12.已知连续函数y=f(x)在区间[1,2]内只有一个零点,为了求这个零点的精确度为0.1的近似值,首先32等分区间[1,2],并将等分点和区间端点1、2按从小到大顺序依次记为x0、x1、x2、x3…x32,然后以[x0,x32](即[1,2])为起始区间,使用二分法逐步逼近寻找符合精确度要求的零点近似值所在区间,如果事实上零点所在区间是(x18,x19),那么按前述方法探求所得的区间应是( )
| A. | (x18,x20) | B. | (x17,x19) | C. | (x16,x20) | D. | (x17,x20) |
10.函数f(x)的定义域为R,f(-1)=2015,对任意的x∈R.都有f′(x)<3x2成立,则不等式f(x)<x3+2016的解集为( )
| A. | (-1,+∞) | B. | (-1,0) | C. | (-∞,-1) | D. | (-∞,+∞) |
9.已知函数f(x)=x2+ax的图象在点A(0,f(0))处的切线l与直线2x-y+2=0平行,若数列{$\frac{1}{f(n)}$}的前n项和为Sn,则S20的值为 ( )
| A. | $\frac{325}{462}$ | B. | $\frac{19}{20}$ | C. | $\frac{119}{256}$ | D. | $\frac{2010}{2011}$ |
5.若点P(1,1)是圆x2+(y-3)2=9的弦AB的中点,则直线AB的方程为 ( )
0 251055 251063 251069 251073 251079 251081 251085 251091 251093 251099 251105 251109 251111 251115 251121 251123 251129 251133 251135 251139 251141 251145 251147 251149 251150 251151 251153 251154 251155 251157 251159 251163 251165 251169 251171 251175 251181 251183 251189 251193 251195 251199 251205 251211 251213 251219 251223 251225 251231 251235 251241 251249 266669
| A. | x-2y+1=0 | B. | x+2y-3=0 | C. | 2x+y-3=0 | D. | 2x-y-1=0 |
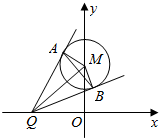 如图,已知圆M:x2+(y-2)2=1,Q是x轴上的动点,QA,QB分别与圆M切于点AB.
如图,已知圆M:x2+(y-2)2=1,Q是x轴上的动点,QA,QB分别与圆M切于点AB.