题目内容
8.求极限$\underset{lim}{n→∞}$$\sqrt{n}$($\sqrt{n+1}$-$\sqrt{n-1}$).分析 化简所求数列的极限的表达式,通过分子有理化,求出极限即可.
解答 解:$\underset{lim}{n→∞}$$\sqrt{n}$($\sqrt{n+1}$-$\sqrt{n-1}$)=$\lim_{n→∞}$$\frac{\sqrt{n}(\sqrt{n+1}-\sqrt{n-1})(\sqrt{n+1}+\sqrt{n-1})}{\sqrt{n+1}+\sqrt{n-1}}$
=$\lim_{n→∞}$$\frac{2\sqrt{n}}{\sqrt{n+1}+\sqrt{n-1}}$
=$\lim_{n→∞}$$\frac{2}{\sqrt{\frac{1}{n}+1}+\sqrt{1-\frac{1}{n}}}$
=1.
点评 本题考查数列的极限的求法,考查计算能力.

练习册系列答案
相关题目
20.从班委会5名成员中选出3名,分别担任班级学习委员、文娱委员与体育委员,其中甲、乙二人不能担任文娱委员,则不同的选法共有( )种.
| A. | 20 | B. | 24. | C. | 36 | D. | 54 |
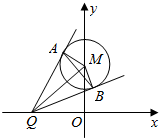 如图,已知圆M:x2+(y-2)2=1,Q是x轴上的动点,QA,QB分别与圆M切于点AB.
如图,已知圆M:x2+(y-2)2=1,Q是x轴上的动点,QA,QB分别与圆M切于点AB.