Question

3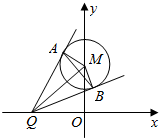．如图，已知圆M：x²+（y-2）²=1，Q是x轴上的动点，QA，QB分别与圆M切于点AB．
（1）若|AB|=$\frac{4\sqrt{2}}{3}$，求直线MQ的方程；
（2）若Q点的坐标为（-2，0），求：
①△AQB外接圆的方程；
②直线AB的方程．

Answer 1

分析 （1）根据P是AB的中点，可求得|MP|，进而利用射影定理可知|MB|²=|MP|•|MQ|求得|MQ|，进而利用勾股定理在Rt△MOQ中，求得|OQ|则Q点的坐标可得，进而可求得MQ的直线方程．
（2）①由题意，△AQB外接圆是以QM为直径的圆，圆心为（-1，1），半径为$\sqrt{2}$，可得△AQB外接圆的方程；
②（x+1）²+（y-1）²=2与x²+（y-2）²=1相减可得直线AB的方程．

解答 解：（1）由P是AB的中点，|AB|=$\frac{4\sqrt{2}}{3}$，
可得|MP|=$\sqrt{1-（\frac{2\sqrt{2}}{3}）^{2}}$=$\frac{1}{3}$．
由射影定理，得|MB|²=|MP|•|MQ|，得|MQ|=3．
在Rt△MOQ中，|OQ|=$\sqrt{{3}^{2}-{2}^{2}}$=$\sqrt{5}$．
故Q点的坐标为（$\sqrt{5}$，0）或（-$\sqrt{5}$，0）．
所以直线MQ的方程是$2x+\sqrt{5}y-2\sqrt{5}$=0或$2x-\sqrt{5}y+2\sqrt{5}$=0．
（2）①由题意，△AQB外接圆是以QM为直径的圆，圆心为（-1，1），半径为$\sqrt{2}$，
∴△AQB外接圆的方程为（x+1）²+（y-1）²=2；
②（x+1）²+（y-1）²=2与x²+（y-2）²=1相减可得直线AB的方程为2x+2y-3=0．

点评 本题主要考查了直线与圆的位置关系，求轨迹方程问题．解题过程中灵活利用了射影定理．