5.将函数y=sin(ωx+φ)(ω>0,|φ|<π)的图象向右平移$\frac{π}{6}$个单位,再将图象上所有点的横坐标伸长到原来的2倍(纵坐标不变)所得的图象解析式为y=sinx,则y=sin(ωx+φ)图象上距离y轴最近的对称轴方程为( )
| A. | x=-$\frac{π}{6}$ | B. | x=$\frac{π}{3}$ | C. | x=-$\frac{π}{12}$ | D. | x=$\frac{π}{12}$ |
4.已知f(x)=Asin(ωx+φ)(A>0,ω>0,x∈R),则“f(x)在x=1处取最大值”是“f(x+1)为偶函数”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
2.如果a<b,那么下列选项正确的是( )
| A. | a+5>b+5 | B. | 3a>3b | C. | -5a>-5b | D. | $\frac{a}{3}$>$\frac{b}{3}$ |
1.如图,在边长为e(e为自然对数的底数)的正方形中,阴影部分的面积为( )


| A. | 2 | B. | $\frac{2}{e}$ | C. | e2 | D. | e |
20.若变量x,y满足约束条件$\left\{\begin{array}{l}x-y+1≤0\\ x+2y-8≤0\\ x≥0\end{array}\right.$,则z=3x+y的最小值为( )
| A. | 3 | B. | 4 | C. | 2 | D. | 1 |
16.投掷一枚均匀硬币和一枚均匀骰子各一次,记“硬币正面向上”为事件A,“骰子向上的点数是3”为事件B,则事件A∪B发生的概率是( )
0 250596 250604 250610 250614 250620 250622 250626 250632 250634 250640 250646 250650 250652 250656 250662 250664 250670 250674 250676 250680 250682 250686 250688 250690 250691 250692 250694 250695 250696 250698 250700 250704 250706 250710 250712 250716 250722 250724 250730 250734 250736 250740 250746 250752 250754 250760 250764 250766 250772 250776 250782 250790 266669
| A. | $\frac{5}{12}$ | B. | $\frac{1}{2}$ | C. | $\frac{7}{12}$ | D. | $\frac{3}{4}$ |
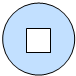 欧阳修《卖油翁》中写到:“(翁)乃取一葫芦置于地,以钱覆其口,徐以杓酌油沥之,自钱孔入,而钱不湿”.可见“行行出状元”,卖油翁的技艺让人叹为观止,如右图铜钱是直径为4cm的圆形,正中间有边长为1cm的正方形孔,若随机向铜钱上滴一滴油(油滴是直径为0.2cm的球),记“油滴不出边界”为事件A,“油滴整体正好落入孔中”为事件B.则P(B|A)=$\frac{64}{361π}$(不作近似值计算).
欧阳修《卖油翁》中写到:“(翁)乃取一葫芦置于地,以钱覆其口,徐以杓酌油沥之,自钱孔入,而钱不湿”.可见“行行出状元”,卖油翁的技艺让人叹为观止,如右图铜钱是直径为4cm的圆形,正中间有边长为1cm的正方形孔,若随机向铜钱上滴一滴油(油滴是直径为0.2cm的球),记“油滴不出边界”为事件A,“油滴整体正好落入孔中”为事件B.则P(B|A)=$\frac{64}{361π}$(不作近似值计算).