若变量x.y满足约束条件$\left\{\begin{array}{l}x-y+1≤0\\ x+2y-8≤0\\ x≥0\end{array}\right.$.则z=3x+y的最小值为( )A．3B．4C．2D．1 题目和参考答案——青夏教育精英家教网——

题目内容

20．若变量x，y满足约束条件$\left\{\begin{array}{l}x-y+1≤0\\ x+2y-8≤0\\ x≥0\end{array}\right.$，则z=3x+y的最小值为（　　）

A．

3

B．

4

C．

2

D．

1

分析由约束条件作出可行域，化目标函数为直线方程的斜截式，数形结合得到最优解，把最优解的坐标代入目标函数得答案．

解答解：由约束条件$\left\{\begin{array}{l}x-y+1≤0\\ x+2y-8≤0\\ x≥0\end{array}\right.$作出可行域如图，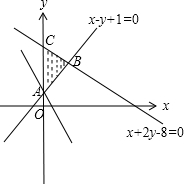

化目标函数z=3x+y为y=-3x+z，
由图可知，当直线y=-3x+z过A（0，1）时，
直线在y轴上的截距最小，z有最小值为1．
故选：D．

点评本题考查线性规划，考查了数形结合的解题思想方法，是中档题．

练习册系列答案

小学毕业班总复习系列答案

小学毕业测试卷系列答案

毕业复习指导系列答案

小学毕业考试标准及复习指导系列答案

考前全程总复习系列答案

培优全真模拟试卷系列答案

五读俱全系列答案

亮点激活精编提优100分大试卷系列答案

同步辅导与能力训练阶段综合测试卷系列答案

小学自评测试系列答案

相关题目

10．设x为实数，[x]表示不大于x的最大整数，如[π]=3，$[{-1.3}]=-2，[{\frac{1}{2}}]=0$，则使[|x-1|]=1成立的x的取值范围是2≤x＜3或-1＜x≤0．

11．定义“等和数列”：在一个数列中，如果每一项与它的后一项的和都为同一常数，那么这个数列叫做等和数列，这个常数叫做该数列的公和，已知数列{a_n}是等和数列，且a₁=2，公和为5，试求：
（1）a₁₈的值；
（2）该数列的前n项和S_n．

8．在数列{a_n}中，已知对任意n∈N^*，a₁+a₂+a₃+…+a_n=3ⁿ-1，则a₁²+a₂²+a₃²+…+a₁₀²=（　　）

（3¹⁰-1）²

$\frac{{{9^{10}}-1}}{2}$

$\frac{{{3^{10}}-1}}{4}$

15．已知数列{a_n}是等差数列，若a₃+a₁₀=10，则S₁₂=（　　）

5．将函数y=sin（ωx+φ）（ω＞0，|φ|＜π）的图象向右平移$\frac{π}{6}$个单位，再将图象上所有点的横坐标伸长到原来的2倍（纵坐标不变）所得的图象解析式为y=sinx，则y=sin（ωx+φ）图象上距离y轴最近的对称轴方程为（　　）

x=-$\frac{π}{6}$

x=$\frac{π}{3}$

x=-$\frac{π}{12}$

x=$\frac{π}{12}$

12．设函数f（x）是定义在R上以2为周期的奇函数，当0≤x≤1时，f（x）=log₂（4x+1），则f（$\frac{13}{4}$）=-2．

9．命题“?x＞0，e^x＜x+1”的否定是?x＞0，e^x≥x+1．

10．给出如下三个命题：
①“x≥2$\sqrt{2}$”是“log₂（x+1）＞2”的充分不必要条件；
②将函数y=sin（2x-$\frac{π}{3}$）的图象向左平移$\frac{π}{6}$个单位可得到函数y=sin2x的图象；
③$\overrightarrow{a}$，$\overrightarrow{b}$为单位向量，其夹角为θ，若|$\overrightarrow{a}$-$\overrightarrow{b}$|＞1，则$\frac{π}{3}$＜θ≤π．
其中正确的命题是②③．（填序号）