12.已知向量|$\overrightarrow{a}$|=1,|$\overrightarrow{b}$|=$\sqrt{2}$,$\overrightarrow{a}$,$\overrightarrow{b}$的夹角为45°,若$\overrightarrow{c}$=$\overrightarrow{a}+\overrightarrow{b}$,$\overrightarrow{d}=\overrightarrow{a}-\overrightarrow{b}$,则$\overrightarrow{c}$在$\overrightarrow{d}$方向上的投影为( )
| A. | 1 | B. | -1 | C. | $\frac{\sqrt{5}}{5}$ | D. | -$\frac{\sqrt{5}}{5}$ |
11.下列结论正确的是( )
| A. | “若a>1,则a2>a”的否命题是“若a>1,则a2≤a” | |
| B. | 对于定义在R上的可导函数f(x),“f′(x0)=0”是“x0为极值点”的充要条件 | |
| C. | “若tanα$≠\sqrt{3}$,则$α≠\frac{π}{3}$”是真命题 | |
| D. | ,?x0∈(-∞,0),使得3${\;}^{{x}_{0}}$<4${\;}^{{x}_{0}}$成立 |
10. 某高中学校为了解中学生的身高情况,从该校同年龄段的所有学生中随机抽取50名学生测量身高,由测量得到频率分布表和频率分布直方图(部分)如下:
某高中学校为了解中学生的身高情况,从该校同年龄段的所有学生中随机抽取50名学生测量身高,由测量得到频率分布表和频率分布直方图(部分)如下:
(1)求m,n并在该题答题纸区域内补全频率分布直方图;
(2)请用这50名学生的身高数据来估计该校这个年龄段的学生身高平均数是多少?(同一组中的数据用该组的中点值作代表);
(3)从[145,155)和[185,195]这两组中任意取出两名学生,求这两名学生身高差距超过10cm的概率.
 某高中学校为了解中学生的身高情况,从该校同年龄段的所有学生中随机抽取50名学生测量身高,由测量得到频率分布表和频率分布直方图(部分)如下:
某高中学校为了解中学生的身高情况,从该校同年龄段的所有学生中随机抽取50名学生测量身高,由测量得到频率分布表和频率分布直方图(部分)如下:| 身高 | [145,155) | [155,165) | [165,175) | [175,185) | [185,195] |
| 频数 | 3 | m | 19 | n | 4 |
(2)请用这50名学生的身高数据来估计该校这个年龄段的学生身高平均数是多少?(同一组中的数据用该组的中点值作代表);
(3)从[145,155)和[185,195]这两组中任意取出两名学生,求这两名学生身高差距超过10cm的概率.
9.已知复数z满足(1+i)•z=2-i(i为虚数单位),则复数z为( )
| A. | $\frac{1}{2}$+$\frac{3}{2}$i | B. | $\frac{1}{2}$-$\frac{3}{2}$i | C. | 1+3i | D. | 1-3i |
7.f(x)为定义在R上的奇函数,其图象关于直线x=$\frac{π}{4}$对称,且当x∈[0,$\frac{π}{4}$]时,f(x)=tan x,则方程5πf(x)-4x=0解的个数是( )
| A. | 7 | B. | 5 | C. | 4 | D. | 3 |
6.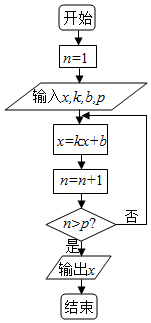 如图所示的程序框图,若输入x,k,b,p的值分别为1,-2,9,3,则输出x的值为( )
如图所示的程序框图,若输入x,k,b,p的值分别为1,-2,9,3,则输出x的值为( )
 如图所示的程序框图,若输入x,k,b,p的值分别为1,-2,9,3,则输出x的值为( )
如图所示的程序框图,若输入x,k,b,p的值分别为1,-2,9,3,则输出x的值为( )| A. | -29 | B. | 19 | C. | 47 | D. | -5 |
5.函数f(x)=lnx-4x+1的递增区间为( )
| A. | ($\frac{1}{4}$,+∞) | B. | (0,4) | C. | (0,$\frac{1}{4}$) | D. | (-∞,$\frac{1}{4}$) |
4.记复数z的共轭复数为$\overline{z}$,若($\overline{z}$+i)(1+i)=2,则复数z所对应的点Z位于复平面的( )
0 241123 241131 241137 241141 241147 241149 241153 241159 241161 241167 241173 241177 241179 241183 241189 241191 241197 241201 241203 241207 241209 241213 241215 241217 241218 241219 241221 241222 241223 241225 241227 241231 241233 241237 241239 241243 241249 241251 241257 241261 241263 241267 241273 241279 241281 241287 241291 241293 241299 241303 241309 241317 266669
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |