11.王府井百货分店今年春节期间,消费达到一定标准的顾客可进行一次抽奖活动,随着抽奖活动的有效开展,参与抽奖活动的人数越来越多,该分店经理对春节前7天参加抽奖活动的人数进行统计,y表示第x天参加抽奖活动的人数,得到统计表格如下:
经过进一步统计分析,发现y与x具有线性相关关系.
(1)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程$\widehaty=\widehatbx+\widehata$;
(2)判断变量x与y之间是正相关还是负相关;
(3)若该活动只持续10天,估计共有多少名顾客参加抽奖.
参与公式:$\widehat{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$,$\widehata=\overline y-\widehatb\overline x$,$\sum_{i=1}^7{{x_i}{y_i}=364}$.
| x | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| y | 5 | 8 | 8 | 10 | 14 | 15 | 17 |
(1)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程$\widehaty=\widehatbx+\widehata$;
(2)判断变量x与y之间是正相关还是负相关;
(3)若该活动只持续10天,估计共有多少名顾客参加抽奖.
参与公式:$\widehat{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$,$\widehata=\overline y-\widehatb\overline x$,$\sum_{i=1}^7{{x_i}{y_i}=364}$.
10. 为了打好脱贫攻坚战,某贫困县农科院针对玉米种植情况进行调研,力争有效地改良玉米品种,为农民提供技术支援.现对已选出的一组玉米的茎高进行统计,获得茎叶图如图(单位:厘米),设茎高大于或等于180厘米的玉米为高茎玉米,否则为矮茎玉米.
为了打好脱贫攻坚战,某贫困县农科院针对玉米种植情况进行调研,力争有效地改良玉米品种,为农民提供技术支援.现对已选出的一组玉米的茎高进行统计,获得茎叶图如图(单位:厘米),设茎高大于或等于180厘米的玉米为高茎玉米,否则为矮茎玉米.
(1)完成2×2列联表,并判断是否可以在犯错误概率不超过1%的前提下,认为抗倒伏与玉米矮茎有关?
(K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d)
(2)为了改良玉米品种,现采用分层抽样的方法从抗倒伏的玉米中抽出5株,再从这5株玉米中选取2株进行杂交试验,选取的植株均为矮茎的概率是多少?
 为了打好脱贫攻坚战,某贫困县农科院针对玉米种植情况进行调研,力争有效地改良玉米品种,为农民提供技术支援.现对已选出的一组玉米的茎高进行统计,获得茎叶图如图(单位:厘米),设茎高大于或等于180厘米的玉米为高茎玉米,否则为矮茎玉米.
为了打好脱贫攻坚战,某贫困县农科院针对玉米种植情况进行调研,力争有效地改良玉米品种,为农民提供技术支援.现对已选出的一组玉米的茎高进行统计,获得茎叶图如图(单位:厘米),设茎高大于或等于180厘米的玉米为高茎玉米,否则为矮茎玉米.(1)完成2×2列联表,并判断是否可以在犯错误概率不超过1%的前提下,认为抗倒伏与玉米矮茎有关?
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(2)为了改良玉米品种,现采用分层抽样的方法从抗倒伏的玉米中抽出5株,再从这5株玉米中选取2株进行杂交试验,选取的植株均为矮茎的概率是多少?
9.运行如下程序框图,分别输入t=45,t=-$\frac{172}{3}$,则输出s的和为( )


| A. | -2017 | B. | 2017 | C. | -2016 | D. | 2016 |
8.若实数x,y满足:|x|≤y≤1,则x2+y2-2x的最小值为( )
| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{2}}}{2}-1$ | C. | $\frac{{\sqrt{2}}}{2}$ | D. | $-\frac{1}{2}$ |
6.某兴趣小组欲研究昼夜温差大小与患感冒人数多少之间的关系,他们分别到气象局与某医院抄录了1至4月份每月10日的昼夜温差情况与因患感冒而就诊的人数,得到如下资料:
(1)请根据1至4月份的数据,求出y关于x的线性回归方程$\widehat{y}$=bx+a;
(2)根据线性回归方程,估计昼夜温差为14℃时,就诊人数为多少人?
(参考公式:b=$\frac{\sum_{i=1}^{4}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{4}({x}_{i}-\overline{x})^{2}}$,a=$\overline{y}$-b$\overline{x}$.)
| 日期 | 昼夜温差x(℃) | 就诊人数y(人) |
| 1月10日 | 11 | 25 |
| 2月10日 | 13 | 29 |
| 3月10日 | 12 | 26 |
| 4月10日 | 8 | 16 |
(2)根据线性回归方程,估计昼夜温差为14℃时,就诊人数为多少人?
(参考公式:b=$\frac{\sum_{i=1}^{4}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{4}({x}_{i}-\overline{x})^{2}}$,a=$\overline{y}$-b$\overline{x}$.)
5.根据回归系数b和回归截距$\widehat{a}$的计算公式可知:若y与x之间的一组数据为:
若拟合这5组数据的回归直线恒经过的点是(4,6),则表中的M的值为7,N的值为7.
| x | 1 | M | 3 | 4 | 5 |
| y | 3 | 5 | 6 | N | 9 |
3. 如图,若N=10,则输出的数等于( )
如图,若N=10,则输出的数等于( )
0 240742 240750 240756 240760 240766 240768 240772 240778 240780 240786 240792 240796 240798 240802 240808 240810 240816 240820 240822 240826 240828 240832 240834 240836 240837 240838 240840 240841 240842 240844 240846 240850 240852 240856 240858 240862 240868 240870 240876 240880 240882 240886 240892 240898 240900 240906 240910 240912 240918 240922 240928 240936 266669
 如图,若N=10,则输出的数等于( )
如图,若N=10,则输出的数等于( )| A. | $\frac{10}{9}$ | B. | $\frac{9}{10}$ | C. | $\frac{10}{11}$ | D. | $\frac{12}{11}$ |
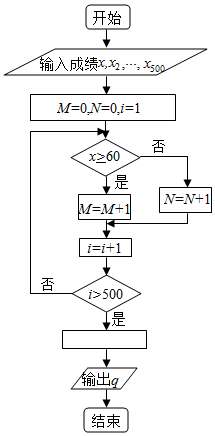 如图是计算某年级500名学生期末考试(满分为100分)及格率q的程序框图,则图中空白框内应填入$q=\frac{M}{M+N}$.
如图是计算某年级500名学生期末考试(满分为100分)及格率q的程序框图,则图中空白框内应填入$q=\frac{M}{M+N}$.