题目内容
8.若实数x,y满足:|x|≤y≤1,则x2+y2-2x的最小值为( )| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{2}}}{2}-1$ | C. | $\frac{{\sqrt{2}}}{2}$ | D. | $-\frac{1}{2}$ |
分析 由实数x,y满足:|x|≤y≤1,可得可行域为:P(1,0),Q点为可行域内的任意一点,当PQ⊥直线y=x时,|PQ|取得最小值,因此|PQ|2取得最小值.
解答 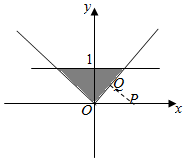 解:由实数x,y满足:|x|≤y≤1,可得可行域为:
解:由实数x,y满足:|x|≤y≤1,可得可行域为:
P(1,0),Q点为可行域内的任意一点,当PQ⊥直线y=x时,
|PQ|取得最小值,因此|PQ|2取得最小值,
则x2+y2-2x=(x-1)2+y2-1≥|PQ|2-1=$(\frac{1-0}{\sqrt{2}})^{2}$-1=-$\frac{1}{2}$.
∴x2+y2-2x的最小值为-$\frac{1}{2}$.
故选:D.
点评 本题考查了线性规划有关知识、点到直线的距离公式、数形结合思想方法,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
8. 已知△ABC满足$AB=4,AC=2,∠BAC=\frac{2π}{3}$,点D、E分别是边AB,BC的中点,连接DE并延长到点F,使得DE=2EF,则 $\overrightarrow{AF}•\overrightarrow{DC}$的值为( )
已知△ABC满足$AB=4,AC=2,∠BAC=\frac{2π}{3}$,点D、E分别是边AB,BC的中点,连接DE并延长到点F,使得DE=2EF,则 $\overrightarrow{AF}•\overrightarrow{DC}$的值为( )
 已知△ABC满足$AB=4,AC=2,∠BAC=\frac{2π}{3}$,点D、E分别是边AB,BC的中点,连接DE并延长到点F,使得DE=2EF,则 $\overrightarrow{AF}•\overrightarrow{DC}$的值为( )
已知△ABC满足$AB=4,AC=2,∠BAC=\frac{2π}{3}$,点D、E分别是边AB,BC的中点,连接DE并延长到点F,使得DE=2EF,则 $\overrightarrow{AF}•\overrightarrow{DC}$的值为( )| A. | -$\frac{3}{2}$ | B. | $\frac{9}{4}$ | C. | -2 | D. | $\frac{5}{2}$ |
3. 如图,若N=10,则输出的数等于( )
如图,若N=10,则输出的数等于( )
 如图,若N=10,则输出的数等于( )
如图,若N=10,则输出的数等于( )| A. | $\frac{10}{9}$ | B. | $\frac{9}{10}$ | C. | $\frac{10}{11}$ | D. | $\frac{12}{11}$ |
13.某医疗科研项目对5只实验小白鼠体内的A、B两项指标数据进行收集和分析,得到的数据如下表:
(1)若通过数据分析,得知A项指标数据与B项指标数据具有线性相关关系,试根据上表,求B项指标数据y关于A项指标数据x的线性回归方程$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$;
(2)现要从这5只小白鼠中随机抽取3只,求其中至少有一只B项指标数据高于3的概率.
参考公式:$\widehat{b}$=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{x}_{i}^{2}-n{\overline{x}}^{2}}$,$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$.
| 指标 | 1号小白鼠 | 2号小白鼠 | 3号小白鼠 | 4号小白鼠 | 5号小白鼠 |
| A | 5 | 7 | 6 | 9 | 8 |
| B | 2 | 2 | 3 | 4 | 4 |
(2)现要从这5只小白鼠中随机抽取3只,求其中至少有一只B项指标数据高于3的概率.
参考公式:$\widehat{b}$=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{x}_{i}^{2}-n{\overline{x}}^{2}}$,$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$.
20.根据如下样本数据
得到的回归方程为${\;}_{y}^{∧}$=${\;}_{b}^{∧}$x+${\;}_{a}^{∧}$,则( )
| 3 | 4 | 5 | 6 | 7 | 8 | |
| y | 4.0 | 2.5 | -0.5 | 0.5 | -2.0 | -3.0 |
| A. | ${\;}_{a}^{∧}$>0,${\;}_{b}^{∧}$>0 | B. | ${\;}_{a}^{∧}$>0,${\;}_{b}^{∧}$<0 | C. | ${\;}_{a}^{∧}$<0,${\;}_{b}^{∧}$>0 | D. | ${\;}_{a}^{∧}$<0,${\;}_{b}^{∧}$<0 |



