14．
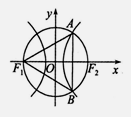F1、F2分别是双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的左右焦点，以坐标原点O为圆心，|OF2|为半径的圆与该双曲线右支交于A、B两点，若△F1AB是等边三角形，则双曲线的离心率为（ ）
F1、F2分别是双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的左右焦点，以坐标原点O为圆心，|OF2|为半径的圆与该双曲线右支交于A、B两点，若△F1AB是等边三角形，则双曲线的离心率为（ ）| A． | $\sqrt{3}$ | B． | 2 | C． | $\sqrt{3}$-1 | D． | 1+$\sqrt{3}$ |
13．若变量x，y满足约束条件$\left\{\begin{array}{l}{y≤x}\\{x+y≤2}\\{y≥-1}\end{array}\right.$，则$\frac{y-2}{x-4}$的取值范围是（ ）
| A． | [0，3] | B． | [$\frac{1}{3}$，3] | C． | [$\frac{4}{3}$，4] | D． | [$\frac{1}{3}$，2] |
12．
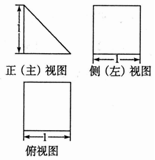某几何体的三视图如图所示，则该几何体的体积为（ ）
某几何体的三视图如图所示，则该几何体的体积为（ ）| A． | $\frac{1}{2}$ | B． | 1 | C． | $\frac{3}{2}$ | D． | 2 |
11．抛物线y2=2px的准线经过点（-2，0），则该抛物线的焦点坐标为（ ）
| A． | （-2，0） | B． | （2，0） | C． | （0，-1） | D． | （0，1） |
9．
如图，在三棱锥P-ABC中，平面PAB⊥平面ABC，△PAB是等边三角形，AC⊥BC，且AC=BC=2，O、D分别是AB，PB的中点．
（1）求证：PA∥平面COD；
（2）求三棱锥P-ABC的体积．
0 240298 240306 240312 240316 240322 240324 240328 240334 240336 240342 240348 240352 240354 240358 240364 240366 240372 240376 240378 240382 240384 240388 240390 240392 240393 240394 240396 240397 240398 240400 240402 240406 240408 240412 240414 240418 240424 240426 240432 240436 240438 240442 240448 240454 240456 240462 240466 240468 240474 240478 240484 240492 266669
如图，在三棱锥P-ABC中，平面PAB⊥平面ABC，△PAB是等边三角形，AC⊥BC，且AC=BC=2，O、D分别是AB，PB的中点．（1）求证：PA∥平面COD；
（2）求三棱锥P-ABC的体积．
如图，甲、乙两名篮球运动员的季后赛10场得分可用茎叶图表示如图：