20.定义$\frac{n}{{p}_{1}+{p}_{2}+…+{p}_{n}}$为n个正数p1,p2,…,pn的“均倒数”.若已知正数数列{an}的前n项的“均倒数”为$\frac{1}{2n+1}$,又bn=$\frac{{a}_{n}+1}{4}$,则$\frac{1}{{b}_{1}{b}_{2}}$+$\frac{1}{{b}_{2}{b}_{3}}$+$\frac{1}{{b}_{3}{b}_{4}}$+…+$\frac{1}{{b}_{2015}{b}_{2016}}$=( )
| A. | $\frac{2013}{2014}$ | B. | $\frac{2014}{2015}$ | C. | $\frac{2015}{2016}$ | D. | $\frac{1}{2015}$ |
19.大衍数列,来源于《乾坤谱》中对易传“大衍之数五十”的推论.主要用于解释中国传统文化中的太极衍生原理.数列中的每一项,都代表太极衍生过程中,曾经经历过的两仪数量总和.是中华传统文化中隐藏着的世界数学史上第一道数列题.其前10项依次是0、2、4、8、12、18、24、32、40、50…,则此数列第20项为( )
| A. | 180 | B. | 200 | C. | 128 | D. | 162 |
18.△ABC中,D,E,F分别是AB,BC,AC的中点,则$\overrightarrow{DF}$=( )
| A. | $\overrightarrow{EF}+\overrightarrow{ED}$ | B. | $\overrightarrow{EF}-\overrightarrow{DE}$ | C. | $\overrightarrow{EF}+\overrightarrow{AD}$ | D. | $\overrightarrow{EF}+\overrightarrow{AF}$ |
16.已知S是△ABC所在平面外的一点,且SA=SB=SC,若S在底面ABC内的射影落在△ABC外部,则△ABC是( )
| A. | 钝角三角形 | B. | 直角三角形 | C. | 锐角三角形 | D. | 以上都有可能 |
15.若 (2x-1)2017=a0+a1x+a2x2+…+a2017x2017(x∈R),则$\frac{1}{2}+\frac{a_2}{{{2^2}{a_1}}}+\frac{a_3}{{{2^3}{a_1}}}+…+\frac{{{a_{2017}}}}{{{2^{2017}}{a_1}}}$=( )
| A. | $\frac{1}{2017}$ | B. | $-\frac{1}{2017}$ | C. | $\frac{1}{4034}$ | D. | $-\frac{1}{4034}$ |
14.设曲线y=ax-ln(2x+1)在点(0,0)处的切线方程为y=2x,则a=( )
0 239982 239990 239996 240000 240006 240008 240012 240018 240020 240026 240032 240036 240038 240042 240048 240050 240056 240060 240062 240066 240068 240072 240074 240076 240077 240078 240080 240081 240082 240084 240086 240090 240092 240096 240098 240102 240108 240110 240116 240120 240122 240126 240132 240138 240140 240146 240150 240152 240158 240162 240168 240176 266669
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
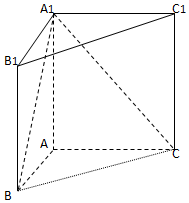 如图,直三棱柱ABC-A1B1C1中,AB=1,AC=AA1=$\sqrt{3}$,∠ABC=60°.
如图,直三棱柱ABC-A1B1C1中,AB=1,AC=AA1=$\sqrt{3}$,∠ABC=60°.