6.已知函数f(x)=$\frac{{4}^{x}-{4}^{-x}}{3}$+log3($\sqrt{{x}^{2}+1}$+x),那么关于x的不等式f(2x-6)+f(x)>0的解集为( )
| A. | {x|x>-2} | B. | {x|x>2} | C. | {x|0<x<2} | D. | {x|-2<x<2} |
5.某汽车的使用年数x与所支出的维修费用y的统计数据如表:
根据上表可得y关于x的线性回归方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x-0.69,若该汽车维修总费用超过10万元就不再维修,直接报废,据此模型预测该汽车最多可使用( )
| 使用年数x(单位:年) | 1 | 2 | 3 | 4 | 5 |
| 维修总费用y(单位:万元) | 0.5 | 1.2 | 2.2 | 3.3 | 4.5 |
| A. | 8年 | B. | 9年 | C. | 10年 | D. | 11年 |
3.直线$\sqrt{2}$ax+by=1与圆x2+y2=1相交于A、B两点(其中a、b是正实数),且△AOB是直角三角形(O是坐标原点),则$\frac{1}{ab}$的最小值为( )
| A. | $\sqrt{2}$ | B. | $\sqrt{2}$+1 | C. | 2 | D. | $\sqrt{2}$-1 |
2.下列函数为奇函数的是( )
| A. | y=$\sqrt{x}$ | B. | y=|sinx| | C. | y=ex-e-x | D. | y=cosx |
20.已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a>0,b>0)的左、右焦点分别为F1,F2,焦距为2c(c>0),抛物线y2=2cx的准线交双曲线左支于A,B两点,且∠AOB=120°,其中O为原点,则双曲线的离心率为( )
| A. | 2 | B. | $1+\sqrt{2}$ | C. | $1+\sqrt{3}$ | D. | $1+\sqrt{5}$ |
19.执行如图所示的程序框图,若m=8,则输出的结果是( )
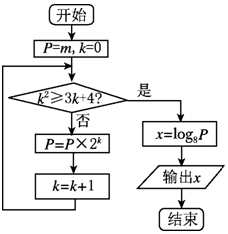

| A. | 2 | B. | $\frac{7}{3}$ | C. | 3 | D. | $\frac{13}{3}$ |
18.已知随机变量ξ服从正态分布N(2,σ2),且P(ξ≤4-a)=P(ξ≥2+3a),则a=( )
0 239868 239876 239882 239886 239892 239894 239898 239904 239906 239912 239918 239922 239924 239928 239934 239936 239942 239946 239948 239952 239954 239958 239960 239962 239963 239964 239966 239967 239968 239970 239972 239976 239978 239982 239984 239988 239994 239996 240002 240006 240008 240012 240018 240024 240026 240032 240036 240038 240044 240048 240054 240062 266669
| A. | -1 | B. | 1 | C. | $\frac{1}{2}$ | D. | $-\frac{1}{2}$ |