20.某电信运营商推出每月资费套餐业务,服务和收费标准如下表:
小明根据自己每月平均主叫时长和使用数据流量的情况(其它费用不计),认为选择58元套餐最省钱,则他每月平均主叫时长和使用数据流量可能为( )
| 套餐费(元) | 免费主叫时长(分钟) | 免费主叫时长收费(元/分钟) | 免费数据流量(MB) | 超出数据流量收费(元/MB) |
| 38 | 50 | 0.25 | 300 | 0.29 |
| 48 | 50 | 0.25 | 500 | 0.29 |
| 58 | 100 | 0.19 | 500 | 0.29 |
| 88 | 220 | 0.19 | 700 | 0.29 |
| A. | 60分钟和300 MB | B. | 70分钟和500 MB | C. | 100分钟和650 MB | D. | 150分钟和550 MB |
19.已知函数f(x)=sin(2x-$\frac{π}{3}$),g(x)=x2-2,若对任意的实数x1,总存在实数x2使得f(x1)=g(x2)成立,则x2的取值范围是( )
| A. | [-1,1] | B. | $[{-\sqrt{3},\sqrt{3}}]$ | C. | (-∞,-1]∪[1,+∞) | D. | [-$\sqrt{3}$,-1]∪[1,$\sqrt{3}$] |
18.设m,n为实数,则“mn>0”是“曲线$\frac{x^2}{m}-\frac{y^2}{n}$=1为双曲线”的( )
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
17.与圆x2+y2+2x-4y=0相切于原点的直线方程是( )
| A. | x-2y=0 | B. | x+2y=0 | C. | 2x-y=0 | D. | 2x+y=0 |
13.某科技公司生产一种手机加密芯片,其质量按测试指标划分为:指标大于或等于70为合格品,小于70为次品.现随机抽取这种芯片共120件进行检测,检测结果统计如表:
已知生产一件芯片,若是合格品可盈利400元,若是次品则亏损50元.
(Ⅰ)试估计生产一件芯片为合格品的概率;并求生产3件芯片所获得的利润不少于700元的概率.
(Ⅱ)记ξ为生产4件芯片所得的总利润,求随机变量ξ的分布列和数学期望.
0 239850 239858 239864 239868 239874 239876 239880 239886 239888 239894 239900 239904 239906 239910 239916 239918 239924 239928 239930 239934 239936 239940 239942 239944 239945 239946 239948 239949 239950 239952 239954 239958 239960 239964 239966 239970 239976 239978 239984 239988 239990 239994 240000 240006 240008 240014 240018 240020 240026 240030 240036 240044 266669
| 测试指标 | [50,60) | [60,70) | [70,80) | [80,90) | [90,100] |
| 芯片数量(件) | 8 | 22 | 45 | 37 | 8 |
(Ⅰ)试估计生产一件芯片为合格品的概率;并求生产3件芯片所获得的利润不少于700元的概率.
(Ⅱ)记ξ为生产4件芯片所得的总利润,求随机变量ξ的分布列和数学期望.
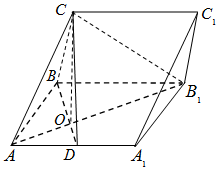 在三棱柱ABC-A1B1C1中,侧面ABB1A1为矩形,AB=2,AA1=2$\sqrt{2}$,D是AA1的中点,BD与AB1交于点O,且CO⊥平面ABB1A1.
在三棱柱ABC-A1B1C1中,侧面ABB1A1为矩形,AB=2,AA1=2$\sqrt{2}$,D是AA1的中点,BD与AB1交于点O,且CO⊥平面ABB1A1.