题目内容
12.已知抛物线y2=2x和圆x2+y2-x=0,倾斜角为$\frac{π}{4}$的直线l经过抛物线的焦点,若直线l与抛物线和圆的交点自上而下依次为A,B,C,D,则|AB|+|CD|=3.分析 由图形可以看出|AB|+|CD|等于弦长AD减去圆的直径,圆的直径易得,弦长AD可由抛物线的性质转化为求两端点A,D到抛物线准线的距离的和,由此求出两点横坐标的和,再求弦长AD.
解答  解:由圆x2+y2-x=0,即(x-$\frac{1}{2}$)2+y2=$\frac{1}{4}$可知,圆心为F($\frac{1}{2}$,0),
解:由圆x2+y2-x=0,即(x-$\frac{1}{2}$)2+y2=$\frac{1}{4}$可知,圆心为F($\frac{1}{2}$,0),
半径为$\frac{1}{2}$,抛物线y2=2x,得到抛物线焦点为F($\frac{1}{2}$,0),如图:
|AB|+|CD|=|AD|-|BC|
∵|BC|为已知圆的直径,∴|BC|=1,则|AB|+|CD|=|AD|-1.
设A(x1,y1)、D(x2,y2),
∵|AD|=|AF|+|FD|,而A、D在抛物线上,
由已知可知,直线l方程为y=x-$\frac{1}{2}$,
由$\left\{\begin{array}{l}{y=x-\frac{1}{2}}\\{{y}^{2}=2x}\end{array}\right.$消去y,得4x2-12x+1=0,
∴x1+x2=3.∴|AD|=3+1=4,
因此,|AB|+|CD|=4-1=3.
故答案为:3.
点评 本题考查直线与圆锥曲线的关系,解题的关键是熟练掌握抛物线的定义与性质,通过这些将求弦长的问题转化为求点到线的距离问题,此转化有一个标志即直线是过焦点的.本题运算量大,极易因为运算出错.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
3.函数y=xsinx(x∈[-π,π])的图象可能是( )
| A. |  | B. |  | C. |  | D. |  |
7.设全集U=R,集合A={y|y=3-x2},B={x|y=log2(x+2)},则(∁UA)∩B=( )
| A. | {x|-2<x≤3} | B. | {x|x>3} | C. | {x|x≥3} | D. | {x|x<-2} |
17.与圆x2+y2+2x-4y=0相切于原点的直线方程是( )
| A. | x-2y=0 | B. | x+2y=0 | C. | 2x-y=0 | D. | 2x+y=0 |
8.已知函数f(x)对任意的x∈R,都有f(-x)+f(x)=-6,且当x≥0时,f(x)=2x-4,则使得f(3x-x2)<0成立的x的取值范围是( )
| A. | (0,3) | B. | (-∞,0)∪(3,+∞) | C. | (1,2) | D. | (-∞,1)∪(2,+∞) |
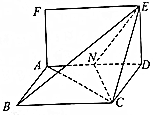 已知矩形ADEF和菱形ABCD所在平面互相垂直,如图,其中AF=1,AD=2,∠ADC=$\frac{π}{3}$,点N时线段AD的中点.
已知矩形ADEF和菱形ABCD所在平面互相垂直,如图,其中AF=1,AD=2,∠ADC=$\frac{π}{3}$,点N时线段AD的中点.