8．已知a=log23.b=log47.$c={0.3^{-\frac{3}{2}}}$.则a.b.c的大小关系为( )A．b＞a＞cB．a＞b＞cC．c＞a＞bD．c＞b＞a——青夏教育精英家教网——

8．已知a=log₂3，b=log₄7，$c={0.3^{-\frac{3}{2}}}$，则a，b，c的大小关系为（　　）

7．随机变量X服从正态分布（3，σ²），且P（X≤4）=0.84，则P（2＜X＜4）=（　　）

6．已知A，B分别是椭圆 $C：\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（{a＞b＞0}）$的长轴与短轴的一个端点，F₁，F₂分别是椭圆C的左、右焦点，D椭圆上的一点，△DF₁，F₂的周长为$6，|{AB}|=\sqrt{7}$．
（1）求椭圆C的方程；
（2）若P是圆x²+y²=7上任一点，过点作P椭圆C的切线，切点分别为M，N，求证：PM⊥PN．

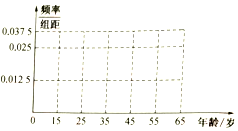随着生活水平的提高，人们对空气质量的要求越来越高，某机构为了解公众对“车辆限行”的态度，随机抽查40人，并将调查情况进行整理后制成如表：

年龄（岁）	[15，25）	[25，35）	[35，45）	[45，55）	[55，65）
频数	5	10	10	5	10
赞成人数	4	6	8	4	9

（1）完成被调查人员年龄的频率分布直方图，并求被调査人员中持赞成态度人员的平均年龄约为多少岁？
（2）若从年龄在[15，25），[45，55）的被调查人员中各随机选取1人进行调查．请写出所有的基本亊件，并求选取2人中恰有1人持不赞成态度的概率．

4．已知函数f（x）满足$f（x）+1=\frac{1}{{f（{x+1}）}}$，当0≤x≤1时，f（x）=x，若方程f（x）-mx-m=0（x∈（-1，1]）有两个不同实数根，则实数m的最大值是（　　）

3．已知抛物线C：y²=2px（p＞0）的焦点为F，准线为l，点P是抛物线C上一点，过P作PM⊥l，垂足为M，记$N（{\frac{7p}{2}，0}），PF$与MN交于点T，若|NF|=2|PF|，且△PNT的面积为$3\sqrt{2}$，则p=（　　）

2．将函数$y=sin（{ωx+φ}）（{ω＞0，|φ|＜\frac{π}{2}}）$的图象沿x轴向左平移$\frac{π}{3}$个单位长度，得到函数$y=cos（{2x+\frac{π}{4}}）$的图象，则φ=（　　）

$\frac{π}{12}$

1．已知直线l：4x+3y-20=0经过双曲线$C：\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$的一个焦点，且与其一条渐近线平行，则双曲线C的实轴长为（　　）

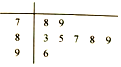
20．佳佳同学在8次测试中，数学成绩的茎叶图如图，则这8次成绩的中位数是（　　）

19．已知函数$f（x）={e^x}-\frac{m}{2}{x^2}-mx-1$．
（1）当m=1时，求证：对?x∈[0，+∞）时，f（x）≥0；
（2）当m≤1时，讨论函数f（x）零点的个数．

0 239721 239729 239735 239739 239745 239747 239751 239757 239759 239765 239771 239775 239777 239781 239787 239789 239795 239799 239801 239805 239807 239811 239813 239815 239816 239817 239819 239820 239821 239823 239825 239829 239831 239835 239837 239841 239847 239849 239855 239859 239861 239865 239871 239877 239879 239885 239889 239891 239897 239901 239907 239915 266669