题目内容
4.已知函数f(x)满足$f(x)+1=\frac{1}{{f({x+1})}}$,当0≤x≤1时,f(x)=x,若方程f(x)-mx-m=0(x∈(-1,1])有两个不同实数根,则实数m的最大值是( )| A. | $-\frac{1}{2}$ | B. | $-\frac{1}{3}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
分析 求出f(x)的解析式,作出f(x)与y=m(x+1)的函数图象,根据图象和交点个数求出m的最大值.
解答 解:当x∈(-1,0)时,f(x)=$\frac{1}{f(x+1)}-1$=$\frac{1}{x+1}-1$,
∵方程f(x)-mx-m=0(x∈(-1,1])有两个不同实数根,
∴f(x)与y=m(x+1)在(-1,1]上有两个交点,
作出f(x)与y=m(x+1)在(-1,1]上的函数图象如图所示:
由图象可知当直线y=m(x+1)经过点(1,1)时,斜率最大,此时m=$\frac{1}{2}$.
故选:D.
点评 本题考查了方程根与函数图象的关系,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
12.已知M为双曲线$C:\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$右支上一点,A,F分别为双曲线C左顶点和的右焦点,MF=AF,若∠MFA=60°,则双曲线C的离心率为( )
| A. | 2 | B. | 3 | C. | 4 | D. | 6 |
9.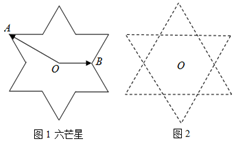 如图2,“六芒星”是由两个全等正三角形组成,中心重合于点O且三组对边分别平行.点A,B是“六芒星”(如图1)的两个顶点,动点P在“六芒星”上(内部以及边界),若$\overrightarrow{OP}=x\overrightarrow{OA}+y\overrightarrow{OB}$,则x+y的取值范围是( )
如图2,“六芒星”是由两个全等正三角形组成,中心重合于点O且三组对边分别平行.点A,B是“六芒星”(如图1)的两个顶点,动点P在“六芒星”上(内部以及边界),若$\overrightarrow{OP}=x\overrightarrow{OA}+y\overrightarrow{OB}$,则x+y的取值范围是( )
 如图2,“六芒星”是由两个全等正三角形组成,中心重合于点O且三组对边分别平行.点A,B是“六芒星”(如图1)的两个顶点,动点P在“六芒星”上(内部以及边界),若$\overrightarrow{OP}=x\overrightarrow{OA}+y\overrightarrow{OB}$,则x+y的取值范围是( )
如图2,“六芒星”是由两个全等正三角形组成,中心重合于点O且三组对边分别平行.点A,B是“六芒星”(如图1)的两个顶点,动点P在“六芒星”上(内部以及边界),若$\overrightarrow{OP}=x\overrightarrow{OA}+y\overrightarrow{OB}$,则x+y的取值范围是( )| A. | [-4,4] | B. | $[{-\sqrt{21},\sqrt{21}}]$ | C. | [-5,5] | D. | [-6,6] |