18.已知向量$\overrightarrow{a}$=(x-1,3),$\overrightarrow{b}$=(1,y),其中x,y都为正实数,若$\overrightarrow{a}⊥\overrightarrow{b}$,则$\frac{1}{x}+\frac{1}{3y}$的最小值为( )
| A. | 2 | B. | 2$\sqrt{2}$ | C. | 4 | D. | 2$\sqrt{3}$ |
17.下列命题中的真命题为( )
| A. | 若向量$\overrightarrow{a}$∥$\overrightarrow{b}$,则存在唯一的实数λ,使得$\overrightarrow{a}$=λ$\overrightarrow{b}$ | |
| B. | 已知随机变量ξ服从正态分布N(1,σ2),若P(ξ≤4)=0.79,则P(ξ≤-2)=0.21 | |
| C. | “φ=$\frac{3π}{2}$”是“y=sin(2x+φ)为偶函数”的充要条件 | |
| D. | 函数y=f(1+x)与函数y=f(1-x)的图象关于直线x=1对称 |
16.对于两个不重合的平面α与β,给定下列条件,其中可以判定α与β平行的条件是( )
| A. | α内有不共线的三点到β的距离相等; | |
| B. | a内存在直线平行于平面β | |
| C. | 存在平面γ,使得α⊥γ,β⊥γ | |
| D. | 存在异面直线l,m使得l∥α,l∥β,m∥α,m∥β |
15. 为了解甲、乙两厂产品的质量,从甲厂生产的产品中随机抽取3件样品,从乙厂生产的产品中随机抽取4件样品,测量产品中某种元素的含量(单位:毫克),如图是测量数据的茎叶图.若它们的中位数相同,平均数也相同,则图中的m,n的比值$\frac{m}{n}$=( )
为了解甲、乙两厂产品的质量,从甲厂生产的产品中随机抽取3件样品,从乙厂生产的产品中随机抽取4件样品,测量产品中某种元素的含量(单位:毫克),如图是测量数据的茎叶图.若它们的中位数相同,平均数也相同,则图中的m,n的比值$\frac{m}{n}$=( )
 为了解甲、乙两厂产品的质量,从甲厂生产的产品中随机抽取3件样品,从乙厂生产的产品中随机抽取4件样品,测量产品中某种元素的含量(单位:毫克),如图是测量数据的茎叶图.若它们的中位数相同,平均数也相同,则图中的m,n的比值$\frac{m}{n}$=( )
为了解甲、乙两厂产品的质量,从甲厂生产的产品中随机抽取3件样品,从乙厂生产的产品中随机抽取4件样品,测量产品中某种元素的含量(单位:毫克),如图是测量数据的茎叶图.若它们的中位数相同,平均数也相同,则图中的m,n的比值$\frac{m}{n}$=( )| A. | 1 | B. | $\frac{1}{3}$ | C. | $\frac{8}{3}$ | D. | $\frac{3}{8}$ |
14.设i为虚数中单位,若复数z=$\frac{a}{1-2i}$+i(a∈R)的实部与虚部互为相反数,则a=( )
| A. | -$\frac{5}{3}$ | B. | -$\frac{1}{3}$ | C. | -1 | D. | -5 |
10.抛物线y2=4x的焦点为F,其准线与x轴的交点为N,过点F作直线与抛物线交于A,B两点,若$\overrightarrow{NB}•\overrightarrow{AB}=0$,则|AF|-|BF|=( )
0 239644 239652 239658 239662 239668 239670 239674 239680 239682 239688 239694 239698 239700 239704 239710 239712 239718 239722 239724 239728 239730 239734 239736 239738 239739 239740 239742 239743 239744 239746 239748 239752 239754 239758 239760 239764 239770 239772 239778 239782 239784 239788 239794 239800 239802 239808 239812 239814 239820 239824 239830 239838 266669
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
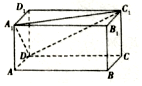 在长方体ABCD-A1B1C1D1中,AB=4,AD=2,AA1=2,点E在棱AB上移动.
在长方体ABCD-A1B1C1D1中,AB=4,AD=2,AA1=2,点E在棱AB上移动.