12．已知函数f（x）=$\left\{\begin{array}{l}{-\frac{3x+2}{x+1}，x∈（-1，0]}\\{x，x∈（0，1]}\end{array}\right.$且g（x）=mx+m，若g（x）=f（x）在（-1，1]内有且仅有两个不同的根，则实数m的取值范围是（ ）
| A． | （-$\frac{9}{4}$，-2]∪（0，$\frac{1}{2}$] | B． | （-$\frac{11}{4}$，-2]∪（0，$\frac{1}{2}$] | C． | （-$\frac{9}{4}$，-2]∪（0，$\frac{2}{3}$] | D． | （-$\frac{11}{4}$，-2]∪（0，$\frac{2}{3}$] |
11．已知函数f（x）满足f（x）=-f（2-x），x∈R，且在[1，+∞）上递增，若g（x）=f（1+x），且2g（log2a）-3g（1）≤g（log${\;}_{\frac{1}{2}}$a），则实数a的范围为（ ）
| A． | （0，2] | B． | （0，$\frac{1}{2}$] | C． | [$\frac{1}{2}$，2] | D． | [2，+∞） |
10．在△ABC中，a，b，c分别为内角A，B，C的对边，且2absinC=$\sqrt{3}$（b2+c2-a2），若a=$\sqrt{13}$，c=3，则△ABC的面积为（ ）
| A． | 3 | B． | 3$\sqrt{3}$ | C． | 2$\sqrt{3}$ | D． | $\frac{3\sqrt{3}}{2}$ |
9．
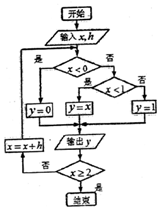如果执行如图的程序框图，输入x=-2，h=2.5，那么输出的各个数的和等于（ ）
如果执行如图的程序框图，输入x=-2，h=2.5，那么输出的各个数的和等于（ ）| A． | 1 | B． | 1.5 | C． | 2.5 | D． | 3 |
8．已知全集为R，且A={x|log2（x+1）＜2}，B={x|$\frac{x-2}{x-1}$≥0}，则A∩（∁RB）等于（ ）
| A． | （-1，1） | B． | （-1，1] | C． | [1，2] | D． | [1，2） |
6．把函数f（x）=cos（2x+φ）的图象上所有的点向左平移$\frac{π}{6}$个单位长度后得到y=g（x）的图象，若y=g（x）的一个对称中心是（$\frac{π}{6}$，0），则φ的一个可能取值是（ ）
0 239573 239581 239587 239591 239597 239599 239603 239609 239611 239617 239623 239627 239629 239633 239639 239641 239647 239651 239653 239657 239659 239663 239665 239667 239668 239669 239671 239672 239673 239675 239677 239681 239683 239687 239689 239693 239699 239701 239707 239711 239713 239717 239723 239729 239731 239737 239741 239743 239749 239753 239759 239767 266669
| A． | $\frac{π}{3}$ | B． | $\frac{7π}{12}$ | C． | $\frac{5π}{6}$ | D． | $\frac{2π}{3}$ |