12.2015年9月3日,抗战胜利70周年纪念活动在北京隆重举行,收到全国人民的瞩目.纪念活动包括举行纪念大会、阅兵式、招待会和文艺晚会等,据统计,抗战老兵由于身体原因,参加纪念大会、阅兵式、招待会这三个环节(可参加多个,也可都不参加)的情况及其概率如表所示:
(1)若m=2n,则从这60名抗战老兵中按照参加纪念活动的环节数分层抽取6人进行座谈,求参加纪念活动环节数为1的抗战老兵中抽取的人数;
(2)某医疗部门决定从(1)中抽取的6名抗战老兵中随机抽取2名进行体检,求这2名抗战老兵中至少有1人参加纪念活动的环节数为3的概率.
| 参加纪念活动的环节数 | 0 | 1 | 2 | 3 |
| 概率 | $\frac{1}{6}$ | m | n | $\frac{1}{3}$ |
(2)某医疗部门决定从(1)中抽取的6名抗战老兵中随机抽取2名进行体检,求这2名抗战老兵中至少有1人参加纪念活动的环节数为3的概率.
10.定义在R上的奇函数f(x)对任意x1,x2(x1≠x2)都有$\frac{{f({x_1})-f({x_2})}}{{{x_1}-{x_2}}}>0$,若实数m,n满足f(m2+4m+12)+f(n2-6n)<0,则|m-2n-4|的取值范围为( )
| A. | $[\frac{{12\sqrt{5}}}{5}-1,\frac{{12\sqrt{5}}}{5}+1]$ | B. | $(\frac{{12\sqrt{5}}}{5}-1,\frac{{12\sqrt{5}}}{5}+1)$ | C. | $[12-\sqrt{5},12+\sqrt{5}]$ | D. | $(12-\sqrt{5},12+\sqrt{5})$ |
9.班主任为了对本班学生的考试成绩进行分析,决定从全班25名男同学,15名女同学中随机抽取一个容量为8的样本进行分析.
(1)如果按性别比例分层抽样,可以得到多少个不同的样本?(只要求写出计算式即可,不
必计算出结果)
(2)随机抽取8位,他们的数学分数从小到大排序是:60,65,70,75,80,85,90,95,物理分数从
小到大排序是:72,77,80,84,88,90,93,95.
①若规定85分以上(包括85分)为优秀,求这8位同学中恰有3位同学的数学和物理分数均
为优秀的概率;
②若这8位同学的数学、物理分数事实上对应如表:
根据上表数据,由变量y与x的相关系数可知物理成绩y与数学成绩x之间具有较强的线性相关关系,现求y与x的线性回归方程(系数精确到0.01).
参考公式:回归直线的方程是:$\stackrel{∧}{y}$=bx+a,其中对应的回归估计值b=$\frac{{\sum_{i=1}^n{({x_i}-\overline x)({y_i}-\overline y)}}}{{\sum_{i=1}^n{{{({x_i}-\overline x)}^2}}}}$,
参考数据:$\overline x=77.5$,$\overline y=84.875$,$\sum_{i=1}^8{{{({x_i}-\overline x)}^2}}$≈1050,$\sum_{i=1}^8{({x_i}-\overline x)({y_i}-\overline y)}$≈688,.
(1)如果按性别比例分层抽样,可以得到多少个不同的样本?(只要求写出计算式即可,不
必计算出结果)
(2)随机抽取8位,他们的数学分数从小到大排序是:60,65,70,75,80,85,90,95,物理分数从
小到大排序是:72,77,80,84,88,90,93,95.
①若规定85分以上(包括85分)为优秀,求这8位同学中恰有3位同学的数学和物理分数均
为优秀的概率;
②若这8位同学的数学、物理分数事实上对应如表:
| 学生编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 数学分数x | 60 | 65 | 70 | 75 | 80 | 85 | 90 | 95 |
| 物理分数y | 72 | 77 | 80 | 84 | 88 | 90 | 93 | 95 |
参考公式:回归直线的方程是:$\stackrel{∧}{y}$=bx+a,其中对应的回归估计值b=$\frac{{\sum_{i=1}^n{({x_i}-\overline x)({y_i}-\overline y)}}}{{\sum_{i=1}^n{{{({x_i}-\overline x)}^2}}}}$,
参考数据:$\overline x=77.5$,$\overline y=84.875$,$\sum_{i=1}^8{{{({x_i}-\overline x)}^2}}$≈1050,$\sum_{i=1}^8{({x_i}-\overline x)({y_i}-\overline y)}$≈688,.
6.若复数z满足(1+2i)2z=1+z,则其共轭复数$\overline{z}$为( )
0 239553 239561 239567 239571 239577 239579 239583 239589 239591 239597 239603 239607 239609 239613 239619 239621 239627 239631 239633 239637 239639 239643 239645 239647 239648 239649 239651 239652 239653 239655 239657 239661 239663 239667 239669 239673 239679 239681 239687 239691 239693 239697 239703 239709 239711 239717 239721 239723 239729 239733 239739 239747 266669
| A. | $\frac{1}{8}$+$\frac{1}{8}$i | B. | -$\frac{1}{8}$-$\frac{1}{8}$i | C. | -$\frac{1}{8}$+$\frac{1}{8}$i | D. | $\frac{1}{8}$-$\frac{1}{8}$i |
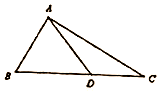 如图,在D是直角△ABC斜边BC上一点,$AC=\sqrt{3}DC$.
如图,在D是直角△ABC斜边BC上一点,$AC=\sqrt{3}DC$.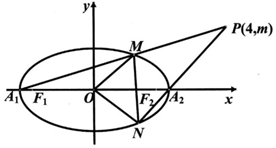 如图,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右项点分别为A1,A2,左右焦点分别为F1,F2,离心率为$\frac{\sqrt{3}}{2}$,|F1F2|=2$\sqrt{3}$,O为坐标原点.
如图,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右项点分别为A1,A2,左右焦点分别为F1,F2,离心率为$\frac{\sqrt{3}}{2}$,|F1F2|=2$\sqrt{3}$,O为坐标原点.