13.设m∈R,过定点A的动直线x+my=0和过定点B的动直线mx-y-m+3=0交于点P(x,y),(点P与点A,B不重合),则△PAB的面积最大值是( )
| A. | $2\sqrt{5}$ | B. | 5 | C. | $\frac{5}{2}$ | D. | $\sqrt{5}$ |
12.某产品的广告费用x(百万元)与销售额y(百万元)的统计数据如表:
根据表中数据,用最小二乘法得出y与x的线性回归方程为$\stackrel{∧}{y}$=8.6x+5,则表中的m的值为( )
| x | 2 | 3 | 4 | 7 | 9 |
| y | 26 | 33 | m | 54 | 75 |
| A. | 46 | B. | 48 | C. | 50 | D. | 52 |
8.已知直线l:x-$\sqrt{3}$y+6=0与圆x2+y2=12交于A,B两点,过A,B分别作l的垂线与x轴交于C,D两点,则|CD|=( )
| A. | $2\sqrt{3}$ | B. | 4 | C. | $4\sqrt{3}$ | D. | 6 |
7.如图为某市2017年2月28天的日空气质量指数折线图.
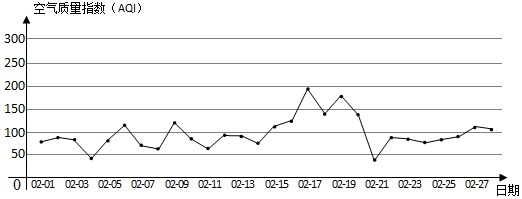
由中国空气质量在线监测分析平台提供的空气质量指数标准如下:
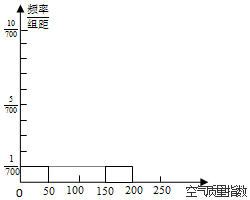
(Ⅰ)请根据所给的折线图补全下方的频率分布直方图(并用铅笔涂黑矩形区域),并估算该市2月份空气质量指数监测数据的平均数(保留小数点后一位);
(Ⅱ)研究人员发现,空气质量指数测评中PM2.5与燃烧排放的CO两个项目存在线性相关关系,以100ug/m3为单位,如表给出PM2.5与CO的相关数据:
求y关于x的回归方程,并估计当CO排放量是200ug/m3时,PM2.5的值.
(用最小二乘法求回归方程的系数是$\hat b=\frac{{\sum_{i=1}^n{{x_i}{y_i}-n•\overline x•\overline y}}}{{\sum_{i=1}^n{x_i^2-n•{{\overline x}^2}}}}$$,\hat a=\overline y-\hat b\overline x$)
0 239503 239511 239517 239521 239527 239529 239533 239539 239541 239547 239553 239557 239559 239563 239569 239571 239577 239581 239583 239587 239589 239593 239595 239597 239598 239599 239601 239602 239603 239605 239607 239611 239613 239617 239619 239623 239629 239631 239637 239641 239643 239647 239653 239659 239661 239667 239671 239673 239679 239683 239689 239697 266669

由中国空气质量在线监测分析平台提供的空气质量指数标准如下:
| 空气质量指数 | (0,50] | (50,100] | (100,150] | (150,200] | (200,300] | 300以上 |
| 空气质量等级 | 1级优 | 2级良 | 3级轻度污染 | 4级中度污染 | 5级重度污染 | 6级严重污染 |

(Ⅱ)研究人员发现,空气质量指数测评中PM2.5与燃烧排放的CO两个项目存在线性相关关系,以100ug/m3为单位,如表给出PM2.5与CO的相关数据:
| CO(x) | 0.5 | 1 | 1.5 |
| PM2.5(y) | 1 | 2 | 4 |
(用最小二乘法求回归方程的系数是$\hat b=\frac{{\sum_{i=1}^n{{x_i}{y_i}-n•\overline x•\overline y}}}{{\sum_{i=1}^n{x_i^2-n•{{\overline x}^2}}}}$$,\hat a=\overline y-\hat b\overline x$)
 将全体正整数ai,j从左向右排成一个直角三角形数阵:
将全体正整数ai,j从左向右排成一个直角三角形数阵: 如图,渔船甲位于岛屿A的南偏西60°方向的B处,且与岛屿A相距6海里,渔船乙以5 海里/小时的速度从岛屿A出发沿正北方向航行,若渔船甲同时从B处出发沿北偏东α的方向追赶渔船乙,刚好用2小时追上.
如图,渔船甲位于岛屿A的南偏西60°方向的B处,且与岛屿A相距6海里,渔船乙以5 海里/小时的速度从岛屿A出发沿正北方向航行,若渔船甲同时从B处出发沿北偏东α的方向追赶渔船乙,刚好用2小时追上.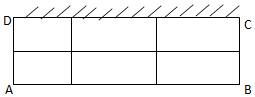 某养猪厂建造一间背面靠墙的长方形猪圈,已知猪圈地面面积为18平方米,将猪圈分割成(如图所示)六个小猪圈,猪圈高度为1米,猪圈每平方米的造价为500元,且不计猪圈背面和地面的费用与猪圈的厚度,问怎样设计总造价最低,最低造价是多少?
某养猪厂建造一间背面靠墙的长方形猪圈,已知猪圈地面面积为18平方米,将猪圈分割成(如图所示)六个小猪圈,猪圈高度为1米,猪圈每平方米的造价为500元,且不计猪圈背面和地面的费用与猪圈的厚度,问怎样设计总造价最低,最低造价是多少?