18.已知定义在R上的函数f(x)满足:①f(x)=f(4-x),②f(x+2)=f(x),③在[0,1]上表达式为f(x)=2x-1,则函数g(x)=f(x)-log3|x|的零点个数为( )
| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
16.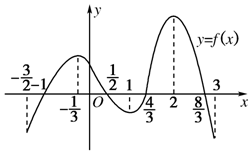 函数y=f(x)在定义域$[{-\frac{3}{2},3}]$内可导,其图象如图所示.记y=f(x)的导函数为y=f′(x),则不等式f′(x)≤0的解集为( )
函数y=f(x)在定义域$[{-\frac{3}{2},3}]$内可导,其图象如图所示.记y=f(x)的导函数为y=f′(x),则不等式f′(x)≤0的解集为( )
 函数y=f(x)在定义域$[{-\frac{3}{2},3}]$内可导,其图象如图所示.记y=f(x)的导函数为y=f′(x),则不等式f′(x)≤0的解集为( )
函数y=f(x)在定义域$[{-\frac{3}{2},3}]$内可导,其图象如图所示.记y=f(x)的导函数为y=f′(x),则不等式f′(x)≤0的解集为( )| A. | $[{-\frac{1}{3},1}]∪[2,3]$ | B. | $[{-1,\frac{1}{2}}]∪[{\frac{4}{3},\frac{8}{3}}]$ | ||
| C. | $[{-\frac{3}{2},\frac{1}{2}}]∪[1,2)$ | D. | $[{-\frac{3}{2},-\frac{1}{3}}]∪[{\frac{1}{2},\frac{4}{3}}]∪[{\frac{4}{3},3}]$ |
15.命题甲:f(x)在区间(a,b)内递增;命题乙:对任意x∈(a,b),有f'(x)>0.则甲是乙的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
11.不等式|x+1|≥kx对任意的x∈R均成立,则k的取值范围是( )
| A. | (-∞,0) | B. | [-1,0] | C. | [0,1] | D. | [0,+∞) |
10.设z1,z2是复数,则下列结论中正确的是( )
| A. | 若${z_1}^2+{z_2}^2>0$,则 ${z_1}^2>-{z_2}^2$ | |
| B. | $|{{z_1}-{z_2}}|=\sqrt{{z_1}^2+{z_2}^2-4{z_1}{z_2}}$ | |
| C. | ${z_1}^2+{z_2}^2=0?{z_1}={z_2}$ | |
| D. | |z1|2=|$\overline{{z}_{1}}$|2 |
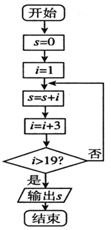
9.根据如图的流程图,可得的结果是( )
0 239321 239329 239335 239339 239345 239347 239351 239357 239359 239365 239371 239375 239377 239381 239387 239389 239395 239399 239401 239405 239407 239411 239413 239415 239416 239417 239419 239420 239421 239423 239425 239429 239431 239435 239437 239441 239447 239449 239455 239459 239461 239465 239471 239477 239479 239485 239489 239491 239497 239501 239507 239515 266669

| A. | 76 | B. | 70 | C. | 51 | D. | 19 |