10．已知$\overrightarrow a=（2，1），\overrightarrow b=（0，-1）$，则$2\overrightarrow b+3\overrightarrow a$=（ ）
| A． | （-6，1） | B． | （6，-1） | C． | （6，1） | D． | （-6，-1） |
9．y=$tan（4x+\frac{π}{3}）$的最小正周期是（ ）
| A． | $\frac{π}{4}$ | B． | $\frac{π}{2}$ | C． | π | D． | 2π |
8．$sin（-\frac{π}{6}）$的值等于（ ）
| A． | $\frac{1}{2}$ | B． | -$\frac{1}{2}$ | C． | $\frac{\sqrt{3}}{2}$ | D． | -$\frac{\sqrt{3}}{2}$ |
7．
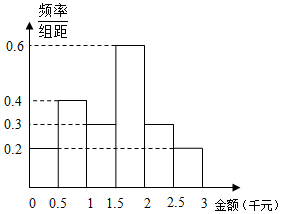某网络营销部门为了统计某市网友2016年12月12日的网购情况，从该市当天参与网购的顾客中随机抽查了男女各30人，统计其网购金额，得到如下频率分布直方图：
若网购金额超过2千元的顾客称为“网购达人”，网购金额不超过2千元的顾客称为“非网购达人”．
（Ⅰ）若抽取的“网购达人”中女性占12人，请根据条件完成上面的2×2列联表，并判断是否有99%的把握认为“网购达人”与性别有关？
（Ⅱ）该营销部门为了进一步了解这60名网友的购物体验，从“非网购达人”、“网购达人”中用分层抽样的方法确定12人，若需从这12人中随机选取3人进行问卷调查．设ξ为选取的3人中“网购达人”的人数，求ξ的分布列和数学期望．
（参考公式：${K^2}=\frac{{n{{（ad-bc）}^2}}}{（a+b）（c+d）（a+c）（b+d）}$，其中n=a+b+c+d）
某网络营销部门为了统计某市网友2016年12月12日的网购情况，从该市当天参与网购的顾客中随机抽查了男女各30人，统计其网购金额，得到如下频率分布直方图：| 网购达人 | 非网购达人 | 合计 | |
| 男性 | 30 | ||
| 女性 | 12 | 30 | |
| 合计 | 60 |
（Ⅰ）若抽取的“网购达人”中女性占12人，请根据条件完成上面的2×2列联表，并判断是否有99%的把握认为“网购达人”与性别有关？
（Ⅱ）该营销部门为了进一步了解这60名网友的购物体验，从“非网购达人”、“网购达人”中用分层抽样的方法确定12人，若需从这12人中随机选取3人进行问卷调查．设ξ为选取的3人中“网购达人”的人数，求ξ的分布列和数学期望．
（参考公式：${K^2}=\frac{{n{{（ad-bc）}^2}}}{（a+b）（c+d）（a+c）（b+d）}$，其中n=a+b+c+d）
| P（K2≥k） | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
5．某市春节期间7家超市广告费支出xi（万元）和销售额yi（万元）数据如表：
（Ⅰ）若用线性回归模型拟合y与x的关系，求y与x的线性回归方程．
（Ⅱ）若用二次函数回归模型拟合y与x的关系，可得回归方程：$\hat y=-0.17{x^2}$+5x+20，经计算二次函数回归模型和线性回归模型的R2分别约为0.93和0.75，请用R2说明选择哪个回归模型更合适，并用此模型预测A超市广告费支出3万元时的销售额．
参考数据：$\overline x=8，\overline y=42，\sum_{i=1}^7{x_i}{y_i}=2794，\sum_{i=1}^7{{x_i}^2}$=708．
参考公式：$\hat b=\frac{{\sum_{i=1}^n{x_i}{y_i}-n\overline x\overline y}}{{\sum_{i=1}^n{{x_i}^2-n{{\overline x}^2}}}}$$，\hat a=\overline y-\hat b\overline x$．
| 超市 | A | B | C | D | E | F | G |
| 广告费支出xi | 1 | 2 | 4 | 6 | 11 | 13 | 19 |
| 销售额yi | 19 | 32 | 40 | 44 | 52 | 53 | 54 |
（Ⅱ）若用二次函数回归模型拟合y与x的关系，可得回归方程：$\hat y=-0.17{x^2}$+5x+20，经计算二次函数回归模型和线性回归模型的R2分别约为0.93和0.75，请用R2说明选择哪个回归模型更合适，并用此模型预测A超市广告费支出3万元时的销售额．
参考数据：$\overline x=8，\overline y=42，\sum_{i=1}^7{x_i}{y_i}=2794，\sum_{i=1}^7{{x_i}^2}$=708．
参考公式：$\hat b=\frac{{\sum_{i=1}^n{x_i}{y_i}-n\overline x\overline y}}{{\sum_{i=1}^n{{x_i}^2-n{{\overline x}^2}}}}$$，\hat a=\overline y-\hat b\overline x$．
4．某商场对A商品近30天的日销售量y（件）与时间t（天）的销售情况进行整理，得到如下数据统计分析，日销售量y（件）与时间t（天）之间具有线性相关关系
（1）请根据表提供的数据，用最小二乘法原理求出y关于t的线性回归方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$t+a
（2）已知A商品近30天内的销售价格Z（元）与时间t（天）的关系为：z=$\left\{\begin{array}{l}{-t+100，（20≤t≤30，t∈N）}\\{t+20，（0＜t＜20，t∈Z）}\end{array}\right.$
根据（1）中求出的线性回归方程，预测t为何值时，A商品的日销售额最大（参考公式$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}{t}_{i}{y}_{i}-n\overline{t}\overline{y}}{\sum_{i=1}^{n}{{t}_{i}}^{2}-n{\overline{t}}^{2}}$，$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}\overline{t}$）
| 时间（t） | 2 | 4 | 6 | 8 | 10 |
| 日销售量（y） | 38 | 37 | 32 | 33 | 30 |
（2）已知A商品近30天内的销售价格Z（元）与时间t（天）的关系为：z=$\left\{\begin{array}{l}{-t+100，（20≤t≤30，t∈N）}\\{t+20，（0＜t＜20，t∈Z）}\end{array}\right.$
根据（1）中求出的线性回归方程，预测t为何值时，A商品的日销售额最大（参考公式$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}{t}_{i}{y}_{i}-n\overline{t}\overline{y}}{\sum_{i=1}^{n}{{t}_{i}}^{2}-n{\overline{t}}^{2}}$，$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}\overline{t}$）
2．《数书九章》中对已知三角形三边长求三角形的面积的求法填补了我国传统数学的一个空白，与著名的海伦公式完全等价，由此可以看出我国古代具有很高的数学水平，其求法是“以小斜幂，并大斜幂，减中斜幂，余半之，自乘于上．以小斜幂乘大斜幂，减上，余四约之，为实，一为从偶，开平方得积”，若把这段文字写成公式，即S=$\sqrt{\frac{1}{4}[{c}^{2}{a}^{2}-（\frac{{c}^{2}+{a}^{2}-{b}^{2}}{2}）^{2}]}$，现有周长为10的△ABC满足sinA：sinB：sin：C=5：7：8，试用以上给出的公式求得△ABC的面积为（ ）
0 239310 239318 239324 239328 239334 239336 239340 239346 239348 239354 239360 239364 239366 239370 239376 239378 239384 239388 239390 239394 239396 239400 239402 239404 239405 239406 239408 239409 239410 239412 239414 239418 239420 239424 239426 239430 239436 239438 239444 239448 239450 239454 239460 239466 239468 239474 239478 239480 239486 239490 239496 239504 266669
| A． | $\frac{5}{8}$ | B． | $\frac{5\sqrt{3}}{2}$ | C． | 10$\sqrt{3}$ | D． | $\frac{35}{8}$ |