题目内容
2.《数书九章》中对已知三角形三边长求三角形的面积的求法填补了我国传统数学的一个空白,与著名的海伦公式完全等价,由此可以看出我国古代具有很高的数学水平,其求法是“以小斜幂,并大斜幂,减中斜幂,余半之,自乘于上.以小斜幂乘大斜幂,减上,余四约之,为实,一为从偶,开平方得积”,若把这段文字写成公式,即S=$\sqrt{\frac{1}{4}[{c}^{2}{a}^{2}-(\frac{{c}^{2}+{a}^{2}-{b}^{2}}{2})^{2}]}$,现有周长为10的△ABC满足sinA:sinB:sin:C=5:7:8,试用以上给出的公式求得△ABC的面积为( )| A. | $\frac{5}{8}$ | B. | $\frac{5\sqrt{3}}{2}$ | C. | 10$\sqrt{3}$ | D. | $\frac{35}{8}$ |
分析 由已知可得a=$\frac{5}{2}$,b=$\frac{7}{2}$,c=$\frac{8}{2}=4$,代入S=$\sqrt{\frac{1}{4}[{c}^{2}{a}^{2}-(\frac{{c}^{2}+{a}^{2}-{b}^{2}}{2})^{2}]}$,即可.
解答 解:周长为10的△ABC满足sinA:sinB:sinC=5:7:8,
则其三边a,b,c满足a:b:c=5:7:8,
设a=5k,b=7k,c=8k,则5k+7k+8k=10,∴a=$\frac{5}{2}$,b=$\frac{7}{2}$,c=$\frac{8}{2}=4$,
代入S=$\sqrt{\frac{1}{4}[{c}^{2}{a}^{2}-(\frac{{c}^{2}+{a}^{2}-{b}^{2}}{2})^{2}]}$,
得s=$\frac{5\sqrt{3}}{2}$,
故选:B
点评 本题考查了正弦定理,解题的关键是要读懂题意,转化条件,属于基础题.

练习册系列答案
相关题目
7.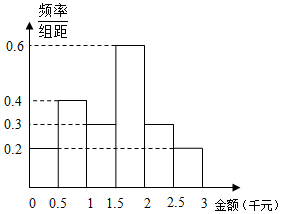 某网络营销部门为了统计某市网友2016年12月12日的网购情况,从该市当天参与网购的顾客中随机抽查了男女各30人,统计其网购金额,得到如下频率分布直方图:
某网络营销部门为了统计某市网友2016年12月12日的网购情况,从该市当天参与网购的顾客中随机抽查了男女各30人,统计其网购金额,得到如下频率分布直方图:
若网购金额超过2千元的顾客称为“网购达人”,网购金额不超过2千元的顾客称为“非网购达人”.
(Ⅰ)若抽取的“网购达人”中女性占12人,请根据条件完成上面的2×2列联表,并判断是否有99%的把握认为“网购达人”与性别有关?
(Ⅱ)该营销部门为了进一步了解这60名网友的购物体验,从“非网购达人”、“网购达人”中用分层抽样的方法确定12人,若需从这12人中随机选取3人进行问卷调查.设ξ为选取的3人中“网购达人”的人数,求ξ的分布列和数学期望.
(参考公式:${K^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d)
 某网络营销部门为了统计某市网友2016年12月12日的网购情况,从该市当天参与网购的顾客中随机抽查了男女各30人,统计其网购金额,得到如下频率分布直方图:
某网络营销部门为了统计某市网友2016年12月12日的网购情况,从该市当天参与网购的顾客中随机抽查了男女各30人,统计其网购金额,得到如下频率分布直方图:| 网购达人 | 非网购达人 | 合计 | |
| 男性 | 30 | ||
| 女性 | 12 | 30 | |
| 合计 | 60 |
(Ⅰ)若抽取的“网购达人”中女性占12人,请根据条件完成上面的2×2列联表,并判断是否有99%的把握认为“网购达人”与性别有关?
(Ⅱ)该营销部门为了进一步了解这60名网友的购物体验,从“非网购达人”、“网购达人”中用分层抽样的方法确定12人,若需从这12人中随机选取3人进行问卷调查.设ξ为选取的3人中“网购达人”的人数,求ξ的分布列和数学期望.
(参考公式:${K^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d)
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
10.函数$y=sinx(\frac{π}{6}≤x≤\frac{π}{2})$的值域是( )
| A. | [-1,1] | B. | $[{\frac{{\sqrt{3}}}{2},1}]$ | C. | $[{\frac{1}{2},\frac{{\sqrt{3}}}{2}}]$ | D. | $[{\frac{1}{2},1}]$ |
 的值域为( )
的值域为( ) B.
B.
 D.
D.
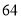 个试室,试室编号为
个试室,试室编号为 ,现根据试室号,采用系统抽样的方法,抽取
,现根据试室号,采用系统抽样的方法,抽取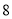 个试室进行监控抽查,已抽看了
个试室进行监控抽查,已抽看了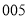 试室号,则下列可能被抽到的试室号是
试室号,则下列可能被抽到的试室号是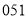 B.
B.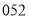 C.
C.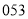 D.
D.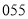
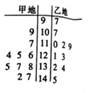 已知在一次期末数学测试中,教育局在某市甲、乙两地各抽取了10名学生的成绩做调查,所的情况如下所示.
已知在一次期末数学测试中,教育局在某市甲、乙两地各抽取了10名学生的成绩做调查,所的情况如下所示.