1.若函数f(x)=sin(2x-$\frac{π}{6}$)的图象向左平移$\frac{π}{6}$个单位后,得到y=g(x)的图象,则下列说法错误的是( )
| A. | y=g(x)的最小正周期为π | B. | y=g(x)的图象关于直线x=$\frac{π}{6}$对称 | ||
| C. | y=g(x)在[-$\frac{π}{6}$,$\frac{π}{3}$]上单调递增 | D. | y=g(x)的图象关于点($\frac{5π}{12}$,0)对称 |
18.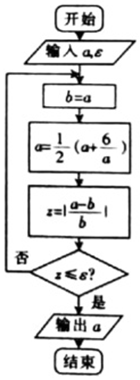 十七世纪英国著名数学家、物理学家牛顿创立的求方程近似解的牛顿迭代法,相较于二分法更具优势,如图给出的是利用牛顿迭代法求方程x2=6的正的近似解的程序框图,若输入a=2,?=0.02,则输出的结果为( )
十七世纪英国著名数学家、物理学家牛顿创立的求方程近似解的牛顿迭代法,相较于二分法更具优势,如图给出的是利用牛顿迭代法求方程x2=6的正的近似解的程序框图,若输入a=2,?=0.02,则输出的结果为( )
 十七世纪英国著名数学家、物理学家牛顿创立的求方程近似解的牛顿迭代法,相较于二分法更具优势,如图给出的是利用牛顿迭代法求方程x2=6的正的近似解的程序框图,若输入a=2,?=0.02,则输出的结果为( )
十七世纪英国著名数学家、物理学家牛顿创立的求方程近似解的牛顿迭代法,相较于二分法更具优势,如图给出的是利用牛顿迭代法求方程x2=6的正的近似解的程序框图,若输入a=2,?=0.02,则输出的结果为( )| A. | 3 | B. | 2.5 | C. | 2.45 | D. | 2.4495 |
13.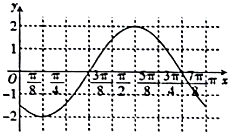 函数f(x)=Asin(ωx+φ)(ω>0,$|φ|<\frac{π}{2}$)的部分图象如图所示,将函数f(x)的图象向右平移$\frac{7π}{24}$个单位后得到函数g(x)的图象,若函数g(x)在区间$[{-\frac{π}{3},θ}]$($θ>-\frac{π}{3}$)上的值域为[-1,2],则θ等于( )
函数f(x)=Asin(ωx+φ)(ω>0,$|φ|<\frac{π}{2}$)的部分图象如图所示,将函数f(x)的图象向右平移$\frac{7π}{24}$个单位后得到函数g(x)的图象,若函数g(x)在区间$[{-\frac{π}{3},θ}]$($θ>-\frac{π}{3}$)上的值域为[-1,2],则θ等于( )
 函数f(x)=Asin(ωx+φ)(ω>0,$|φ|<\frac{π}{2}$)的部分图象如图所示,将函数f(x)的图象向右平移$\frac{7π}{24}$个单位后得到函数g(x)的图象,若函数g(x)在区间$[{-\frac{π}{3},θ}]$($θ>-\frac{π}{3}$)上的值域为[-1,2],则θ等于( )
函数f(x)=Asin(ωx+φ)(ω>0,$|φ|<\frac{π}{2}$)的部分图象如图所示,将函数f(x)的图象向右平移$\frac{7π}{24}$个单位后得到函数g(x)的图象,若函数g(x)在区间$[{-\frac{π}{3},θ}]$($θ>-\frac{π}{3}$)上的值域为[-1,2],则θ等于( )| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{2π}{3}$ | D. | $\frac{7π}{12}$ |
12.已知复数z=(2+i)(a+2i3)在复平面内对应的点在第四象限,则实数a的取值范围是( )
0 239157 239165 239171 239175 239181 239183 239187 239193 239195 239201 239207 239211 239213 239217 239223 239225 239231 239235 239237 239241 239243 239247 239249 239251 239252 239253 239255 239256 239257 239259 239261 239265 239267 239271 239273 239277 239283 239285 239291 239295 239297 239301 239307 239313 239315 239321 239325 239327 239333 239337 239343 239351 266669
| A. | (-∞,-1) | B. | (4,+∞) | C. | (-1,4) | D. | (-4,-1) |
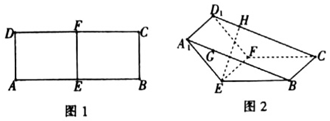 如图1,在矩形ABCD中,AB=8,AD=3,点E、F分别为AB、CD的中点,将四边形AEFD沿EF折到A1EFD1的位置,使∠A1EB=120°,如图2所示,点G,H分别在A1B,D1C上,A1G=D1H=$\sqrt{3}$,过点G,H的平面α与几何体A1EB-D1FC的面相交,交线围成一个正方形.
如图1,在矩形ABCD中,AB=8,AD=3,点E、F分别为AB、CD的中点,将四边形AEFD沿EF折到A1EFD1的位置,使∠A1EB=120°,如图2所示,点G,H分别在A1B,D1C上,A1G=D1H=$\sqrt{3}$,过点G,H的平面α与几何体A1EB-D1FC的面相交,交线围成一个正方形.