4.下列函数中,值域为[0,+∞)的偶函数是( )
| A. | y=x2-1 | B. | y=|x| | C. | y=lgx | D. | y=cosx |
3.若函数f(x)的定义域为R,则“函数f(x)是奇函数”是“f(0)=0”的( )
| A. | 必要不充分条件 | B. | 既不充分也不必要条件 | ||
| C. | 充要条件 | D. | 充分不必要条件 |
1.由于空气污染严重,某工厂生产了两种供人们外出时便于携带的呼吸装置,其质量按测试指标划分:指标大于或等于82为合格品,小于82为次品.现随机抽取这两种装置各100件进行检测,检测结果统计如下:
(Ⅰ)试分别估计装置甲、装置乙为合格品的概率;
(Ⅱ)生产一件装置甲,若是合格品可盈利40元,若是次品则亏损5元;生产一件装置乙,若是合格品可盈利50元,若是次品则亏损10元.在(Ⅰ)的条件下,
(1)记X为生产一件装置甲和生产一件装置乙所得的总利润,求随机变量X的分布列和数学期望;
(2)求生产5件装置乙所获得的利润不少于140元的概率.
| 测试指标 | [70,76] | [76,82] | [82,88] | [88,94] | [94,100] |
| 装置甲 | 8 | 12 | 40 | 32 | 8 |
| 装置乙 | 7 | 18 | 40 | 29 | 6 |
(Ⅱ)生产一件装置甲,若是合格品可盈利40元,若是次品则亏损5元;生产一件装置乙,若是合格品可盈利50元,若是次品则亏损10元.在(Ⅰ)的条件下,
(1)记X为生产一件装置甲和生产一件装置乙所得的总利润,求随机变量X的分布列和数学期望;
(2)求生产5件装置乙所获得的利润不少于140元的概率.
17.设函数f(x)=ex+a+x,g(x)=ln(x+3)-4e-x-a,其中e为自然对数的底数,若存在实数x0,使得f(x0)-g(x0)=2成立,则实数a值为( )
| A. | -2+ln2 | B. | 1+ln2 | C. | -1-ln2 | D. | 2+ln2 |
16.已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左右焦点分别为F1,F2,点P在双曲线的右支上,且|PF1|=5|PF2|,则此双曲线的离心率的取值范围是( )
| A. | (1,$\sqrt{3}$] | B. | (1,$\frac{3}{2}$] | C. | [$\frac{3}{2}$,+∞) | D. | (3,+∞) |
15.设偶函数y=2sin(ωx+φ)(ω>0,0<φ<π)的图象与直线y=2的某两个交点的横坐标分别为x1,x2,若|x2-x1||的最小值为π,则该函数在下列哪个区间上单调递增( )
0 239118 239126 239132 239136 239142 239144 239148 239154 239156 239162 239168 239172 239174 239178 239184 239186 239192 239196 239198 239202 239204 239208 239210 239212 239213 239214 239216 239217 239218 239220 239222 239226 239228 239232 239234 239238 239244 239246 239252 239256 239258 239262 239268 239274 239276 239282 239286 239288 239294 239298 239304 239312 266669
| A. | (0,$\frac{π}{2}$) | B. | (-$\frac{π}{4}$,$\frac{π}{4}$) | C. | (-$\frac{π}{2}$,-$\frac{π}{4}$) | D. | ($\frac{π}{4}$,$\frac{3π}{4}$) |
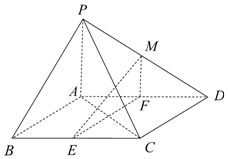 如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,∠BCD=135°,侧面PAB⊥底面ABCD,∠BAP=90°,AB=AC=PA=2,E,F分别为BC,AD的中点,点M在线段PD上.
如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,∠BCD=135°,侧面PAB⊥底面ABCD,∠BAP=90°,AB=AC=PA=2,E,F分别为BC,AD的中点,点M在线段PD上.