4.定义在R上的函数f(x)满足f(x+4)=f(x),f(x)=$\left\{\begin{array}{l}-{x^2}+1,\;\;-1≤x≤1\\-|{x-2}|+1,\;1<x≤3\end{array}$.若关于x的方程f(x)-ax=0有5个不同实根,则正实数a的取值范围是( )
| A. | $({\frac{1}{4},\frac{1}{3}})$ | B. | $({\frac{1}{6},\frac{1}{4}})$ | C. | $({16-6\sqrt{7},\frac{1}{6}})$ | D. | $({\frac{1}{6},8-2\sqrt{15}})$ |
3.由直线y=x+2上的点向圆(x-4)2+(y+2)2=1引切线,则切线长的最小值为( )
| A. | $4\sqrt{2}$ | B. | $\sqrt{31}$ | C. | $\sqrt{33}$ | D. | $4\sqrt{2}-1$ |
1.已知函数f(x)=$\sqrt{3}$sin(2x+φ)+cos(2x+φ)为偶函数,且在[0,$\frac{π}{4}$]上是增函数,则φ的一个可能值为( )
| A. | $\frac{π}{3}$ | B. | $\frac{2π}{3}$ | C. | $\frac{4π}{3}$ | D. | $\frac{5π}{3}$ |
20.为调查我市居民对“文明出行”相关规定的了解情况,某媒体随机选取了30名行人进行问卷调查,将他们的年龄整理后分组,制成下表:
己知从中任选一人,年龄在(12,22]的频率为0.3
(I)求m,n的值;
(II)通过问卷得知,参与调查的52岁以上的两个组中,了解相关规定的人各占$\frac{1}{2}$.现从这两个组中任选2人,求选取的2人都了解相关规定的概率.
0 239024 239032 239038 239042 239048 239050 239054 239060 239062 239068 239074 239078 239080 239084 239090 239092 239098 239102 239104 239108 239110 239114 239116 239118 239119 239120 239122 239123 239124 239126 239128 239132 239134 239138 239140 239144 239150 239152 239158 239162 239164 239168 239174 239180 239182 239188 239192 239194 239200 239204 239210 239218 266669
| 年龄(岁) | (12,22] | (22,32] | (32,42] | (42,52] | (52,62] | (62,72] |
| 频数 | m | 3 | 7 | 5 | 4 | n |
(I)求m,n的值;
(II)通过问卷得知,参与调查的52岁以上的两个组中,了解相关规定的人各占$\frac{1}{2}$.现从这两个组中任选2人,求选取的2人都了解相关规定的概率.
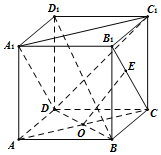 在棱长为1的正方体ABCD-A1B1C1D1中,AC∩BD=O,E是线段B1C(含端点)上的一动点,则
在棱长为1的正方体ABCD-A1B1C1D1中,AC∩BD=O,E是线段B1C(含端点)上的一动点,则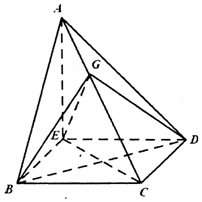 如图,在三棱锥A-BCD中,∠ABC=∠BCD=∠CDA=90°,AC=6$\sqrt{3}$,BC=CD=6,E点在平面BCD内,EC=BD,EC⊥BD.
如图,在三棱锥A-BCD中,∠ABC=∠BCD=∠CDA=90°,AC=6$\sqrt{3}$,BC=CD=6,E点在平面BCD内,EC=BD,EC⊥BD.