题目内容
17.已知点A(-2,3)在抛物线C:y2=2px的准线上,过点A的直线与C在第一象限相切于点B,记C的焦点为F,则|BF|=10.分析 由题意先求出准线方程x=-2,再求出p,从而得到抛物线方程,写出第一象限的抛物线方程,设出切点,并求导,得到切线AB的斜率,再由两点的斜率公式得到方程,解出方程求出切点,再由两点的距离公式可求得.
解答 解:∵点A(-2,3)在抛物线C:y2=2px的准线上,
即准线方程为:x=-2,
∴p>0,-$\frac{p}{2}$=-2即p=4,
∴抛物线C:y2=8x,在第一象限的方程为y=2$\sqrt{2x}$,
设切点B(m,n),则n=2$\sqrt{2m}$,
又导数y′=2$\sqrt{2}•\frac{1}{2}•\frac{1}{\sqrt{x}}$,则在切点处的斜率为$\frac{\sqrt{2}}{\sqrt{m}}$,
∴$\frac{n-3}{m+2}$=$\frac{\sqrt{2}}{\sqrt{m}}$,即$\sqrt{m}$m+2$\sqrt{2}$=2$\sqrt{2}$-3$\sqrt{m}$,
解得:$\sqrt{m}$=2$\sqrt{2}$或($\frac{\sqrt{2}}{2}$舍去),
∴切点B(8,8),又F(2,0),
∴|BF|=$\sqrt{36+64}$=10.
故答案为:10.
点评 本题主要考查抛物线的方程和性质,同时考查直线与抛物线相切,运用导数求切线的斜率等,是一道中档题.

练习册系列答案
相关题目
8.已知直线a⊥平面α,则“直线b∥平面α”是“直线a⊥直线b”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
6.设i是虚数单位,复数$z=\frac{{2{i^3}}}{1-i}$,则复数z的共轭复数为( )
| A. | -1+i | B. | -1-i | C. | 1-i | D. | 1+i |
9.设α∈(0,$\frac{π}{2}$),若sinα=$\frac{3}{5}$,则$\sqrt{2}cos(2α+\frac{π}{4})$=( )
| A. | $\frac{7}{25}$ | B. | $\frac{17}{25}$ | C. | -$\frac{17}{25}$ | D. | $\frac{31}{25}$ |
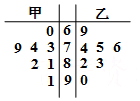 某人到甲、乙两市各7个小区调查空置房情况,调查得到的小区空置房的套数绘成了如图的茎叶图,则调查中甲市空置房套数的中位数与乙市空置房套数的中位数之差为( )
某人到甲、乙两市各7个小区调查空置房情况,调查得到的小区空置房的套数绘成了如图的茎叶图,则调查中甲市空置房套数的中位数与乙市空置房套数的中位数之差为( ) 在四棱锥P-ABCD中,AD∥BC,AD=AB=DC=$\frac{1}{2}$BC=1,E是PC的中点,面PAC⊥面ABCD.
在四棱锥P-ABCD中,AD∥BC,AD=AB=DC=$\frac{1}{2}$BC=1,E是PC的中点,面PAC⊥面ABCD.