16.某公司要推出一种新产品,分6个相等时长的时段进行试销,并对卖出的产品进行跟踪以及收集顾客的评价情况(包括产品评价和服务评价),在试销阶段共卖出了480件,通过对所卖出产品的评价情况和销量情况进行统计,一方面发现对该产品的好评率为$\frac{5}{6}$,对服务的好评率为0.75,对产品和服务两项都没有好评有30件,另一方面发现销量和单价有一定的线性相关关系,具体数据如下表:
(1)能否在犯错误的概率不超过0.001的前提下,认为产品好评和服务好评有关?
(2)该产品的成本是500元/件,预计在今后的销售中,销量和单价仍然服从这样的线性相关关系($\widehat{y}$=$\widehat{b}$x+$\widehat{a}$),该公司如果想获得最大利润,此产品的定价应为多少元?
(参考公式:线性回归方程$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$中系数计算公式分别为:$\widehat{b}$=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$,$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$;K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d)
(参考数据
$\sum_{n=1}^{6}$xiyi=406600,$\sum_{n=1}^{6}$xi2=4342000)
0 239008 239016 239022 239026 239032 239034 239038 239044 239046 239052 239058 239062 239064 239068 239074 239076 239082 239086 239088 239092 239094 239098 239100 239102 239103 239104 239106 239107 239108 239110 239112 239116 239118 239122 239124 239128 239134 239136 239142 239146 239148 239152 239158 239164 239166 239172 239176 239178 239184 239188 239194 239202 266669
| 时段 | 1 | 2 | 3 | 4 | 5 | 6 |
| 单价x(元) | 800 | 820 | 840 | 860 | 880 | 900 |
| 销量y(件) | 90 | 84 | 83 | 80 | 75 | 68 |
(2)该产品的成本是500元/件,预计在今后的销售中,销量和单价仍然服从这样的线性相关关系($\widehat{y}$=$\widehat{b}$x+$\widehat{a}$),该公司如果想获得最大利润,此产品的定价应为多少元?
(参考公式:线性回归方程$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$中系数计算公式分别为:$\widehat{b}$=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$,$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$;K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d)
(参考数据
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
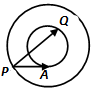 如图同心圆中,大、小圆的半径分别为2和1,点P在大圆上,PA与小圆相切于点A,Q为小圆上的点,则$\overrightarrow{PA}•\overrightarrow{PQ}$的取值范围是[3-$\sqrt{3}$,3+$\sqrt{3}$].
如图同心圆中,大、小圆的半径分别为2和1,点P在大圆上,PA与小圆相切于点A,Q为小圆上的点,则$\overrightarrow{PA}•\overrightarrow{PQ}$的取值范围是[3-$\sqrt{3}$,3+$\sqrt{3}$].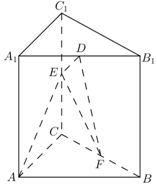 如图,在直棱柱ABC-A1B1C1中,AA1=AB=AC=2,AB⊥AC,D,E,F分别是A1B1,CC1,BC的中点.
如图,在直棱柱ABC-A1B1C1中,AA1=AB=AC=2,AB⊥AC,D,E,F分别是A1B1,CC1,BC的中点.