题目内容
2.直线$\left\{\begin{array}{l}x=2+t\;\\ y=4-t\end{array}\right.$(t为参数)与曲线$\left\{\begin{array}{l}x=3+\sqrt{2}cosθ\;\\ y=5+\sqrt{2}sinθ\end{array}\right.$(θ为参数)的公共点的个数是1.分析 根据题意,将直线的参数方程变形为普通方程,再将曲线的参数方程变形为普通方程,分析可得该曲线为圆,且圆心坐标为(3,5),半径r=$\sqrt{2}$,求出圆心到直线的俄距离,分析可得直线与圆相切,即可得直线与圆有1个公共点,即可得答案.
解答 解:根据题意,直线的参数方程为$\left\{\begin{array}{l}x=2+t\;\\ y=4-t\end{array}\right.$,则其普通方程为x+y-6=0,
曲线的参数方程为$\left\{\begin{array}{l}x=3+\sqrt{2}cosθ\;\\ y=5+\sqrt{2}sinθ\end{array}\right.$,则其普通方程为(x-3)2+(y-5)2=2,该曲线为圆,且圆心坐标为(3,5),半径r=$\sqrt{2}$,
圆心到直线x+y-6=0的距离d=$\frac{|3+5-6|}{\sqrt{1+1}}$=$\sqrt{2}$=r,
则圆(x-3)2+(y-5)2=2与直线x+y-6=0相切,有1个公共点;
故答案为:1.
点评 本题考查直线与圆的参数方程,关键是将圆和直线的参数方程变形为普通方程.

练习册系列答案
 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
10.$\frac{1-i}{1+i}$=( )
| A. | -i | B. | i | C. | 1 | D. | -1 |
7. 某公司为了解广告投入对销售收益的影响,在若干地区各投入4万元广告费用,并将各地的销售收益绘制成频率分布直方图(如图所示).由于工作人员操作失误,横轴的数据丢失,但可以确定横轴是从0开始计数的.[附:回归直线的斜率和截距的最小二乘估计公式分别为$\widehat{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$,$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$.
某公司为了解广告投入对销售收益的影响,在若干地区各投入4万元广告费用,并将各地的销售收益绘制成频率分布直方图(如图所示).由于工作人员操作失误,横轴的数据丢失,但可以确定横轴是从0开始计数的.[附:回归直线的斜率和截距的最小二乘估计公式分别为$\widehat{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$,$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$.
(1)根据频率分布直方图计算图中各小长方形的宽度;
(2)试估计该公司投入4万元广告费用之后,对应销售收益的平均值(以各组的区间中点值代表该组的取值);
(3)该公司按照类似的研究方法,测得另外一些数据,并整理得到下表:
由表中的数据显示,x与y之间存在着线性相关关系,请将(2)的结果填入空白栏,并求出y关于x的回归直线方程.
 某公司为了解广告投入对销售收益的影响,在若干地区各投入4万元广告费用,并将各地的销售收益绘制成频率分布直方图(如图所示).由于工作人员操作失误,横轴的数据丢失,但可以确定横轴是从0开始计数的.[附:回归直线的斜率和截距的最小二乘估计公式分别为$\widehat{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$,$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$.
某公司为了解广告投入对销售收益的影响,在若干地区各投入4万元广告费用,并将各地的销售收益绘制成频率分布直方图(如图所示).由于工作人员操作失误,横轴的数据丢失,但可以确定横轴是从0开始计数的.[附:回归直线的斜率和截距的最小二乘估计公式分别为$\widehat{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$,$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$.(1)根据频率分布直方图计算图中各小长方形的宽度;
(2)试估计该公司投入4万元广告费用之后,对应销售收益的平均值(以各组的区间中点值代表该组的取值);
(3)该公司按照类似的研究方法,测得另外一些数据,并整理得到下表:
| 广告投入x(单位:万元) | 1 | 2 | 3 | 4 | 5 |
| 销售收益y(单位:万元) | 2 | 3 | 2 | 7 |
14.函数$y={log_{\frac{1}{3}}}({-{x^2}+2x+3})$的单调增区间是( )
| A. | (-1,1] | B. | (-∞,1) | C. | [1,3) | D. | (1,+∞) |
12.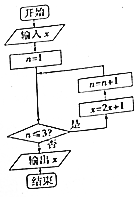 阅读右边程序框图,当输入的值为3时,运行相应程序,则输出x的值为( )
阅读右边程序框图,当输入的值为3时,运行相应程序,则输出x的值为( )
 阅读右边程序框图,当输入的值为3时,运行相应程序,则输出x的值为( )
阅读右边程序框图,当输入的值为3时,运行相应程序,则输出x的值为( )| A. | 7 | B. | 15 | C. | 31 | D. | 63 |