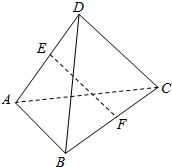
17.已知点M是圆C:(x-1)2+(y-4)2=1上的点,不等式组$\left\{\begin{array}{l}{x+2y+4≥0}\\{x+4y≤0}\\{x+(a-1)y+2(a-1)≤0}\\{\;}\end{array}\right.$(a≠1)表示的平面区域为Ω,点P是Ω上一点,若|PM|的最小值为$\sqrt{17}$-1,则实数a的取值范围为( )
| A. | (-∞,1) | B. | (-3,1) | C. | (1,+∞) | D. | (1,3) |
16.双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左右焦点分别为F1,F2,Q为右支上一点,P点在直线x=-a上,且满足$\overrightarrow{PQ}$=$\overrightarrow{Q{F}_{2}}$,$\overrightarrow{OQ}$=λ($\frac{\overrightarrow{O{F}_{2}}}{|\overrightarrow{O{F}_{2}}|}$+$\frac{\overrightarrow{OP}}{|\overrightarrow{OP}|}$)(λ≠0),则该双曲线的离心率为( )
| A. | $\sqrt{5}$+1 | B. | $\sqrt{2}$+1 | C. | 2 | D. | $\sqrt{2}$ |
12.把函数f(x)=2sin(2x+$\frac{π}{6}$)的图象沿x轴向左平移$\frac{π}{6}$个长度单位,得到函数g(x)的图象,关于函数g(x),下列说法正确的是( )
| A. | 在[$\frac{π}{4}$,$\frac{π}{2}$]上是增函数 | |
| B. | 其图象关于直线x=-$\frac{π}{4}$对称 | |
| C. | 函数g(x)是奇函数 | |
| D. | 当x∈[$\frac{π}{6}$,$\frac{2π}{3}$]时,函数g(x)的值域是[-2,1] |
10.已知函数f(x)=$\left\{\begin{array}{l}{{x}^{2}+ax,x≤1}\\{-x-3,x>1}\end{array}\right.$,则“a≤-2”是“f(x)在R上单调函数”的( )
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
9.执行下图的程序框图,若输入的a,b,k分别是2,1,3,则输出的M=( )
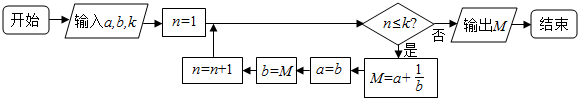
0 225061 225069 225075 225079 225085 225087 225091 225097 225099 225105 225111 225115 225117 225121 225127 225129 225135 225139 225141 225145 225147 225151 225153 225155 225156 225157 225159 225160 225161 225163 225165 225169 225171 225175 225177 225181 225187 225189 225195 225199 225201 225205 225211 225217 225219 225225 225229 225231 225237 225241 225247 225255 266669
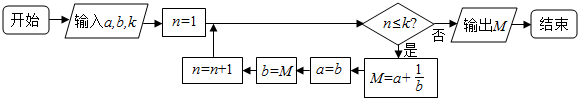
| A. | $\frac{4}{3}$ | B. | $\frac{8}{5}$ | C. | $\frac{15}{4}$ | D. | $\frac{15}{8}$ |