3.已知函数f(x)=2sin(ωx+φ)+1(0<ω<3,0<φ<$\frac{π}{2}$)的一系列对应值如下表:
(1)根据表格提供的数据求函败y=f(x)的解析式;
(2)求函数y=f(x)的单调递增区间与对称中心坐标;
(3)函数y=mf(x)-1在(-$\frac{π}{12}$,$\frac{π}{3}$)上有零点,求实数m的取值范围.
| x | -$\frac{π}{3}$ | -$\frac{π}{12}$ | 0 | $\frac{π}{6}$ | $\frac{5π}{12}$ | $\frac{2π}{3}$ | $\frac{11π}{12}$ |
| f(x) | -1 | 1 | 2 | 3 | 1 | -1 | 1 |
(2)求函数y=f(x)的单调递增区间与对称中心坐标;
(3)函数y=mf(x)-1在(-$\frac{π}{12}$,$\frac{π}{3}$)上有零点,求实数m的取值范围.
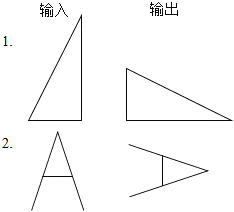
17.己知某种输入输出映射关系如图:定义该输出输出的映射关系为f,则f(|)=( )
0 225006 225014 225020 225024 225030 225032 225036 225042 225044 225050 225056 225060 225062 225066 225072 225074 225080 225084 225086 225090 225092 225096 225098 225100 225101 225102 225104 225105 225106 225108 225110 225114 225116 225120 225122 225126 225132 225134 225140 225144 225146 225150 225156 225162 225164 225170 225174 225176 225182 225186 225192 225200 266669

| A. | - | B. | / | C. | | | D. | \ |
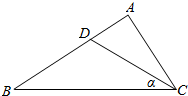 在△ABC中,BC=2AC,cosC=$\frac{3}{5}$,D是AB上的点,∠BCD=α,S△ACD:S△BCD=1:2.
在△ABC中,BC=2AC,cosC=$\frac{3}{5}$,D是AB上的点,∠BCD=α,S△ACD:S△BCD=1:2.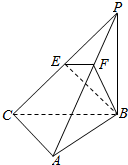 如图,三棱锥P-ABC中,PB⊥底面ABC,∠BCA=90°,PB=BC=CA=2,E为PC的中点,M为AB的中点,点F在PA上,且2PF=FA.
如图,三棱锥P-ABC中,PB⊥底面ABC,∠BCA=90°,PB=BC=CA=2,E为PC的中点,M为AB的中点,点F在PA上,且2PF=FA.