题目内容
19.已知函数f(x)是定义域在R上的奇函数,且在区间(-∞,0]单调递减,求满足f(x2+2x-3)>f(-x2-4x+5)的x的集合.分析 根据条件可以判断f(x)在R上单调递减,从而由f(x2+2x-3)>f(-x2-4x+5)便可得到x2+2x-3<-x2-4x+5,这样解出该不等式便可得出满足f(x2+2x-3)>f(-x2-4x+5)的x的集合.
解答 解:∵f(x)为奇函数,在(-∞,0]上单调递减;
∴f(x)在[0,+∞)上单调递减;
∴f(x)在R上单调递减;
∴由f(x2+2x-3)>f(-x2-4x+5)得:x2+2x-3<-x2-4x+5;
解得-4<x<1;
∴满足f(x2+2x-3)>f(-x2-4x+5)的x的集合为(-4,1).
点评 考查奇函数的定义,以及奇函数在对称区间上的单调性特点,减函数的定义,一元二次不等式的解法.

练习册系列答案
相关题目
7.设曲线y=2016xn+1(n∈N*)在点(1,2016)处的切线与x轴交点的横坐标为xn,令an=log2016xn,则a1+a2+…+a2015的值为( )
| A. | 2016 | B. | 2015 | C. | 1 | D. | -1 |
14.将45化为二进制正确的是( )
| A. | 111001 | B. | 110111 | C. | 101101 | D. | 111011 |
11.下面四个条件中,使a>b成立的充要条件是( )
| A. | |a|>|b| | B. | $\frac{1}{a}$>$\frac{1}{b}$ | C. | a2>b2 | D. | 2a>2b |
9.“命题p为真命题”是“命题p∨q为真命题”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分又不必要条件 |
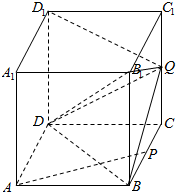 如图,正方体ABCD-A1B1C1D1的棱长为2,P是BC的中点,点Q是棱CC1上的动点.
如图,正方体ABCD-A1B1C1D1的棱长为2,P是BC的中点,点Q是棱CC1上的动点.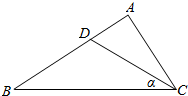 在△ABC中,BC=2AC,cosC=$\frac{3}{5}$,D是AB上的点,∠BCD=α,S△ACD:S△BCD=1:2.
在△ABC中,BC=2AC,cosC=$\frac{3}{5}$,D是AB上的点,∠BCD=α,S△ACD:S△BCD=1:2.