1.某初级中学有学生270人,其中一年级108人,二、三年级各81人,现要利用抽样方法抽取10人参加某项调查,考虑选用简单随机抽样、分层抽样和系统抽样三种方案.使用简单随机抽样和分层抽样时,将学生按一、二、三年级依次统一编号为1,2,…,270;使用系统抽样时,将学生统一随机编号为1,2,…,270,并将整个编号依次分为10段.如果抽得的号码有下列四种情况:
①7,34,61,88,115,142,169,196,223,250;
②5,9,100,107,111,121,180,195,200,265;
③11,38,65,92,119,146,173,200,227,254;
④30,57,84,111,138,165,192,219,246,270.
关于上述样本的下列结论中正确的是( )
①7,34,61,88,115,142,169,196,223,250;
②5,9,100,107,111,121,180,195,200,265;
③11,38,65,92,119,146,173,200,227,254;
④30,57,84,111,138,165,192,219,246,270.
关于上述样本的下列结论中正确的是( )
| A. | ②③都不可能为系统抽样 | B. | ②④都不可能为分层抽样 | ||
| C. | ①④都可能为系统抽样 | D. | ①③都可能为分层抽样 |
17.如图所示是一个几何体的三视图,则这个几何体的表面积为( )
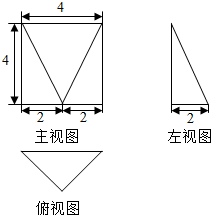

| A. | $20+4\sqrt{2}+4\sqrt{5}$ | B. | $20+8\sqrt{2}$ | C. | $20+8\sqrt{2}+4\sqrt{5}$ | D. | $20+4\sqrt{5}$ |
16.已知函数f(x)=sinx+cosx,且f′(x)=3f(x),则tan2x的值是( )
| A. | -$\frac{4}{3}$ | B. | $\frac{4}{3}$ | C. | -$\frac{3}{4}$ | D. | $\frac{3}{4}$ |
15.若向量$\overrightarrow{a}$、$\overrightarrow{b}$满足$\overrightarrow{a}$=(1,2),$\overrightarrow{b}$=(1,-3),则向量$\overrightarrow{a}$与$\overrightarrow{b}$的夹角等于( )
| A. | $\frac{π}{4}$ | B. | $\frac{π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{3π}{4}$ |
14.为调查某地区老年人是否需要志愿者提供帮助,用简单随机抽样方法从该地区调查了500位老人,结果如下面表中所示:
(1)请根据上表的数据,估计该地区老年人中,需要志愿者提供帮助的老年人的比例;
(2)能否在出错的概率不超过1%的前提下,认为该地老年人是否需要帮助与性别有关?并说明理由;
(3)根据(2)的结论,你能否提出更好的调查方法来估计该地区的老年人中,需要志愿者提供帮助的老年人的比例?并说明理由.
附:独立性检验卡方统计量${K^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d为样本容量,独立性检验临界值表为:
0 224563 224571 224577 224581 224587 224589 224593 224599 224601 224607 224613 224617 224619 224623 224629 224631 224637 224641 224643 224647 224649 224653 224655 224657 224658 224659 224661 224662 224663 224665 224667 224671 224673 224677 224679 224683 224689 224691 224697 224701 224703 224707 224713 224719 224721 224727 224731 224733 224739 224743 224749 224757 266669
| 性别 是否需要帮助 | 男 | 女 | 合计 |
| 需要 | 50 | 25 | 75 |
| 不需要 | 200 | 225 | 425 |
| 合计 | 250 | 250 | 500 |
(2)能否在出错的概率不超过1%的前提下,认为该地老年人是否需要帮助与性别有关?并说明理由;
(3)根据(2)的结论,你能否提出更好的调查方法来估计该地区的老年人中,需要志愿者提供帮助的老年人的比例?并说明理由.
附:独立性检验卡方统计量${K^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d为样本容量,独立性检验临界值表为:
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |