8．
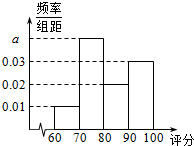某生产车间为了检测其加工的零件的质量，检验人员需抽取同批次的零件样本进行检测指标评分．若检测指标评分大于60分的零件为合格零件，指标评分不超过40分的零件将直接被淘汰，指标评分在（40，60]内的零件可能被修复也可能被淘汰．现质检员小张检测出200个合格零件，根据指标评分绘制的频率分布直方图如图所示，
（1）求出频率分布直方图中a的值；
（2）估计这200个零件指标评分的平均数和中位数；
（Ⅱ）根据已有的经验，可能被修复的零件个体被修复的概率如下表：
假设每个零件被修复与否相互独立．现有3个零件的检测指标评分（单位：分）为：38，45，52，
①求这3个零件中，至多有2个不被修复而淘汰的概率；
②记这3个零件被修复的个数为随机变量X，求X的分布列和数学期望．
0 224508 224516 224522 224526 224532 224534 224538 224544 224546 224552 224558 224562 224564 224568 224574 224576 224582 224586 224588 224592 224594 224598 224600 224602 224603 224604 224606 224607 224608 224610 224612 224616 224618 224622 224624 224628 224634 224636 224642 224646 224648 224652 224658 224664 224666 224672 224676 224678 224684 224688 224694 224702 266669
某生产车间为了检测其加工的零件的质量，检验人员需抽取同批次的零件样本进行检测指标评分．若检测指标评分大于60分的零件为合格零件，指标评分不超过40分的零件将直接被淘汰，指标评分在（40，60]内的零件可能被修复也可能被淘汰．现质检员小张检测出200个合格零件，根据指标评分绘制的频率分布直方图如图所示，（1）求出频率分布直方图中a的值；
（2）估计这200个零件指标评分的平均数和中位数；
（Ⅱ）根据已有的经验，可能被修复的零件个体被修复的概率如下表：
| 零件检测指标评分所在区间 | （40，50] | （50，60] |
| 每个零件个体被修复的概率 | $\frac{1}{3}$ | $\frac{1}{2}$ |
①求这3个零件中，至多有2个不被修复而淘汰的概率；
②记这3个零件被修复的个数为随机变量X，求X的分布列和数学期望．