��Ŀ����
8��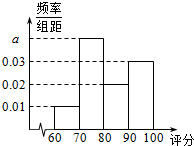 ij��������Ϊ�˼����ӹ��������������������Ա���ȡͬ���ε�����������м��ָ�����֣������ָ�����ִ���60�ֵ����Ϊ�ϸ������ָ�����ֲ�����40�ֵ������ֱ�ӱ���̭��ָ�������ڣ�40��60]�ڵ�������ܱ���Ҳ���ܱ���̭�����ʼ�ԱС�ż���200���ϸ����������ָ�����ֻ��Ƶ�Ƶ�ʷֲ�ֱ��ͼ��ͼ��ʾ��
ij��������Ϊ�˼����ӹ��������������������Ա���ȡͬ���ε�����������м��ָ�����֣������ָ�����ִ���60�ֵ����Ϊ�ϸ������ָ�����ֲ�����40�ֵ������ֱ�ӱ���̭��ָ�������ڣ�40��60]�ڵ�������ܱ���Ҳ���ܱ���̭�����ʼ�ԱС�ż���200���ϸ����������ָ�����ֻ��Ƶ�Ƶ�ʷֲ�ֱ��ͼ��ͼ��ʾ����1�����Ƶ�ʷֲ�ֱ��ͼ��a��ֵ��
��2��������200�����ָ�����ֵ�ƽ��������λ����
���������еľ��飬���ܱ�����������屻���ĸ������±���
| ������ָ�������������� | ��40��50] | ��50��60] |
| ÿ��������屻���ĸ��� | $\frac{1}{3}$ | $\frac{1}{2}$ |
������3������У�������2������������̭�ĸ��ʣ�
�ڼ���3����������ĸ���Ϊ�������X����X�ķֲ��к���ѧ������
���� ��1����Ƶ�ʷֲ�ֱ��ͼ�и�С�������֮��Ϊ1�������a��
��2������Ƶ�ʷֲ�ֱ��ͼ�ܹ�����200�����ָ�����ֵ�ƽ��������λ����
������3������У�������2������������̭�Ķ����¼�����3�����ȫ����������̭���ɴ����ö����¼����ʼ��㹫ʽ�������3������У�������2������������̭�ĸ��ʣ�
������֪��X�Ŀ���ȡֵΪ0��1��2���ֱ������Ӧ�ĸ��ʣ��ɴ������X�ķֲ��к���ѧ������
��� �⣺��1����Ƶ�ʷֲ�ֱ��ͼ���ã�
��0.01+a+0.02+0.03����10=1��
���a=0.04��
��2��������200�����ָ�����ֵ�ƽ����$\overline{x}$=10����65��0.01+75��0.04+85��0.02+95��0.03��=82��
��Ƶ�ʷֲ�ֱ��ͼ����ǰ����С���ε����֮��Ϊ0.5��
�������200�����ָ�����ֵ���λ��Ϊ80��
������3������У�������2������������̭�Ķ����¼�����3�����ȫ����������̭��
����3������У�������2������������̭�ĸ��ʣ�
p=1-$��1-\frac{1}{3}����1-\frac{1}{2}��$=$\frac{2}{3}$��
������֪��X�Ŀ���ȡֵΪ0��1��2��
P��X=0��=$��1-\frac{1}{3}����1-\frac{1}{2}��$=$\frac{1}{3}$��
P��X=1��=$\frac{1}{3}����1-\frac{1}{2}��+��1-\frac{1}{3}����\frac{1}{2}$=$\frac{1}{2}$��
P��X=2��=$\frac{1}{3}��\frac{1}{2}$=$\frac{1}{6}$��
��X�ķֲ���Ϊ��
| X | 0 | 1 | 2 |
| P | $\frac{1}{3}$ | $\frac{1}{2}$ | $\frac{1}{6}$ |
���� ���⿼��Ƶ�ʷֲ�ֱ��ͼ��Ӧ�ã�������ʵ���������ɢ����������ķֲ��к���ѧ�����������е��⣬����ʱҪ�������⣬������߿��ж��DZؿ�����֮һ��

 ����ѧ����ϵ�д�
����ѧ����ϵ�д�