15．函数$f(x)=\frac{1}{{\sqrt{x-1}}}+\frac{1}{x-3}$的定义域为．——青夏教育精英家教网——

15．函数$f（x）=\frac{1}{{\sqrt{x-1}}}+\frac{1}{x-3}$的定义域为（1，3）∪（3．+∞）．

14．已知集合A={1，2，3，4，5}，则集合A的子集的个数为32．

13．已知$1＞{（{\frac{1}{2}}）^n}＞{（{\frac{1}{2}}）^m}$，则下列关系正确的是（　　）

12．函数y=（a²-5a+5）a^x是指数函数，则a的值为（　　）

11．下列函数中，既是奇函数又是增函数的是（　　）

	A．	y=x\|x\|		B．	y=x²，x∈[-1，1]
	C．	$y=-\frac{1}{x}，x∈[{-1，0}）∪（{0，1}）$		D．	y=x+1

10．下列各对函数中，图象完全相同的是（　　）

	A．	y=x与$y=\sqrt{x^2}$		B．	y=x⁰与$y=\frac{x}{x}$
	C．	y=\|x\|与$y={\|{\sqrt{x}}\|^2}$		D．	$y=\sqrt{x+1}\sqrt{x-1}$与$y=\sqrt{（{x+1}）（{x-1}）}$

9．若集合A={-1，1}，B={x|mx=1}，且A∩B=B，则m的值是（　　）

8．设集合$A=\left\{{\left.x\right|x≤4}\right\}，m=\sqrt{3}+\sqrt{2}$，则下列关系中正确的是（　　）

7．某企业生产某种产品，在2011年至2015年所获利润（单位：十万元）的数据如下表：

年份	2011	2012	2013	2014	2015
年份代号t	1	2	3	4	5
利润y	5.8	6.6	7.1	7.4	8.1

（Ⅰ）求y关于t的线性回归方程；
（Ⅱ）利用（Ⅰ）中的回归方程，分析2011年至2015年该企业所获利润的变化情况，并预测该企业在2016年的所获利润．附：回归直线的斜率和截距的最小二乘法估计公式分别为：$\widehat{b}$=$\frac{\sum_{i=1}^{n}（{t}_{i}-\overline{t}）（{y}_{i}-\overline{y}）}{\sum_{i=1}^{n}（{t}_{i}-\overline{t}）^{2}}$，$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{t}$．

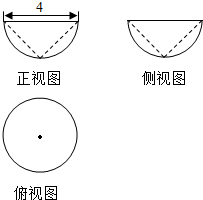如图为一个半球挖去一个圆锥后的几何体的三视图，则剩余部分与挖去部分的体积之比为（　　）

0 224232 224240 224246 224250 224256 224258 224262 224268 224270 224276 224282 224286 224288 224292 224298 224300 224306 224310 224312 224316 224318 224322 224324 224326 224327 224328 224330 224331 224332 224334 224336 224340 224342 224346 224348 224352 224358 224360 224366 224370 224372 224376 224382 224388 224390 224396 224400 224402 224408 224412 224418 224426 266669