19.设不等式组 $\left\{\begin{array}{l}{x-2y+2≥0}\\{3x-2y-3≤0}\\{x+y-1≥0}\end{array}\right.$,表示的平面区域为D,P(x,y)∈D,若x2+y2≥m恒成立,则实数m的最大值为( )
| A. | $\frac{1}{2}$ | B. | $\frac{3}{4}$ | C. | $\frac{4}{5}$ | D. | $\frac{5}{6}$ |
18.已知数列{an}的前n项和Sn=$\frac{1}{2}$n(n+1),n∈N*,bn=3n+(-1)n-1an,则数列{bn}的前2n+1项和为( )
0 224130 224138 224144 224148 224154 224156 224160 224166 224168 224174 224180 224184 224186 224190 224196 224198 224204 224208 224210 224214 224216 224220 224222 224224 224225 224226 224228 224229 224230 224232 224234 224238 224240 224244 224246 224250 224256 224258 224264 224268 224270 224274 224280 224286 224288 224294 224298 224300 224306 224310 224316 224324 266669
| A. | $\frac{{3}^{2n+2}-1}{2}$+n | B. | $\frac{1}{2}$•32n+2+n+$\frac{1}{2}$ | C. | $\frac{{3}^{2n+2}-1}{2}$-n | D. | $\frac{1}{2}$•32n+2-n+$\frac{3}{2}$ |
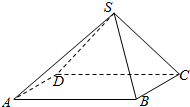 如图所示,在四棱锥S-ABCD中,底面ABCD是矩形,侧面SDC⊥底面ABCD,求证:平面SCD⊥平面SBC.
如图所示,在四棱锥S-ABCD中,底面ABCD是矩形,侧面SDC⊥底面ABCD,求证:平面SCD⊥平面SBC.