题目内容
1.若0<x1<x2<1,则下列判断正确的有③.①e${\;}^{{x}_{2}}$-e${\;}^{{x}_{1}}$>lnx2-lnx1;②e${\;}^{{x}_{2}}$-e${\;}^{{x}_{1}}$<lnx2-lnx1;③x2e${\;}^{{x}_{1}}$>x1e${\;}^{{x}_{2}}$;④x2e${\;}^{{x}_{1}}$<x1e${\;}^{{x}_{2}}$.
分析 分别构造函数f(x)=ex-lnx,g(x)=$\frac{{e}^{x}}{x}$,利用导数判断f(x),g(x)在(0,1)上的单调性,根据单调性即可比较.
解答 解:令f(x)=ex-lnx,g(x)=$\frac{{e}^{x}}{x}$,
∴f′(x)=ex-$\frac{1}{x}$,g′(x)=$\frac{(x-1){e}^{x}}{{x}^{2}}$
∵0<x1<x2<1
∴f′(x)的符号不确定,g′(x)<0,
∴f(x)在(0,1)上的单调性有增有减,g(x)在(0,1)上单调递减,
∴f(x1)与f(x2)无法比较大小,g(x1)>g(x2),
∴e${\;}^{{x}_{2}}$-lnx2与e${\;}^{{x}_{1}}$-lnx1无法比较,$\frac{{e}^{{x}_{1}}}{{x}_{1}}$>$\frac{{e}^{{x}_{2}}}{{x}_{2}}$,
即x2e${\;}^{{x}_{1}}$>x1e${\;}^{{x}_{2}}$,
故答案为:③
点评 本题考查利用导数研究函数的单调性,考查了函数构造法,解答此题的关键在于想到构造两个函数.

练习册系列答案
相关题目
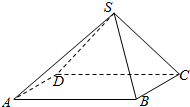 如图所示,在四棱锥S-ABCD中,底面ABCD是矩形,侧面SDC⊥底面ABCD,求证:平面SCD⊥平面SBC.
如图所示,在四棱锥S-ABCD中,底面ABCD是矩形,侧面SDC⊥底面ABCD,求证:平面SCD⊥平面SBC.