题目内容
18.已知数列{an}的前n项和Sn=$\frac{1}{2}$n(n+1),n∈N*,bn=3n+(-1)n-1an,则数列{bn}的前2n+1项和为( )| A. | $\frac{{3}^{2n+2}-1}{2}$+n | B. | $\frac{1}{2}$•32n+2+n+$\frac{1}{2}$ | C. | $\frac{{3}^{2n+2}-1}{2}$-n | D. | $\frac{1}{2}$•32n+2-n+$\frac{3}{2}$ |
分析 由n=1时,a1=S1,n>1时,an=Sn-Sn-1,求得an=n,再由数列的求和方法:分组求和,结合等比数列的求和公式,计算即可得到所求值.
解答 解:前n项和Sn=$\frac{1}{2}$n(n+1),可得n=1时,a1=S1=1,
n>1时,an=Sn-Sn-1=$\frac{1}{2}$n(n+1)-$\frac{1}{2}$(n-1)n=n,
即有an=n,n∈N*,bn=3n+(-1)n-1an=3n+(-1)n-1•n,
则数列{bn}的前2n+1项和为(3+9+…+32n+1)+[1-2+3-4+5-6+…+(2n+1)]
=$\frac{3(1-{3}^{2n+1})}{1-3}$+(-n)+(2n+1)=$\frac{{3}^{2n+2}-1}{2}$+n.
故选A.
点评 本题考查数列的通项的求法,注意运用数列的通项和前n项和的关系,考查等差数列和等比数列的求和公式的运用,属于中档题.

练习册系列答案
 巧学巧练系列答案
巧学巧练系列答案
相关题目
8.已知向量$\overrightarrow m=(sin2x,1)$,$\overrightarrow n=(cos2x,-\frac{3}{2})$,$f(x)=(\overrightarrow m-\overrightarrow n)•\overrightarrow m$,则函数f(x)的最小正周期与最大值分别为( )
| A. | $π,3+\frac{{\sqrt{2}}}{2}$ | B. | $\frac{π}{2},3+\frac{{\sqrt{2}}}{2}$ | C. | $π,\frac{7}{2}$ | D. | $\frac{π}{2},3$ |
7. 已知某几何体的三视图如图所示,则该几何体的体积为( )
已知某几何体的三视图如图所示,则该几何体的体积为( )
 已知某几何体的三视图如图所示,则该几何体的体积为( )
已知某几何体的三视图如图所示,则该几何体的体积为( )| A. | 4 | B. | 6 | C. | 8 | D. | 10 |
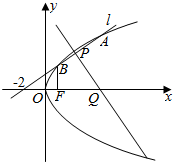 如图,设抛物线y2=4x的焦点为F,过点(-2,0)的直线l交抛物线于A,B两点,线段AB的中垂线分别与AB,x轴交于P,Q两点.若P,Q,F,B四点共圆,则该圆的半径是$\frac{\sqrt{65}}{4}$.
如图,设抛物线y2=4x的焦点为F,过点(-2,0)的直线l交抛物线于A,B两点,线段AB的中垂线分别与AB,x轴交于P,Q两点.若P,Q,F,B四点共圆,则该圆的半径是$\frac{\sqrt{65}}{4}$.