6.设f(x)=ax2+bx+c(a>0)满足f(1+x)=f(1-x),则f(2x)与f(3x)的大小关系为( )
| A. | f (3x)≥f (2x) | B. | f (3x)≤f (2x) | C. | f (3x)<f (2x) | D. | 不确定 |
4.某运输公司接受了向四川地震灾区每天至少运送180t支援物资的任务.该公司有8辆载重6t的A型卡车与4辆载重为10t的B型卡车,有10名驾驶员,每辆卡车每天往返的次数是A型卡车4次,B型卡车3次;每辆卡车往返的成本费是A型卡车320元,B型卡车504元.
(1)设所需A型、B型卡车分别为x辆和y辆,每天A型车和B型车往返的成本费之和为z,请完成如表的空格;
(2)请为公司安排一下,应如何调配车辆,才能使公司所花的往返成本费最低?
(1)设所需A型、B型卡车分别为x辆和y辆,每天A型车和B型车往返的成本费之和为z,请完成如表的空格;
| A型车 | B型车 | 限量 | |
| 车辆数 | x | y | 0≤x≤8,0≤y≤4 |
| 每天运物吨数 | 24x | 30y | 24x+30y≥180 |
| 每天往返成本费 | 320x | 504y | z |
3.为了解篮球爱好者小李的投篮命中率与打篮球时间之间的关系,下表记录了小李某月1号到5号每天打篮球时间x单位:小时)与当天投篮命中率y之间的关系:
(1)求小李这5天的平均投篮命中率;
(2)用线性回归分析的方法,预测小李该月6号打6小时篮球的投篮命中率.$\left\{\begin{array}{l}\hat b=\frac{{\sum_{i=1}^n{({x_i}-\overline x)({y_i}-\overline y)}}}{{\sum_{i=1}^n{{{({x_i}-\overline x)}^2}}}}=\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x\overline y}}}{{\sum_{i=1}^n{x_i^2-n{{\overline x}^2}}}}\\ \hat a=\overline y-\hat b\overline x\end{array}\right.$.
| 时间x | 1 | 2 | 3 | 4 | 5 |
| 命中率y | 0.4 | 0.5 | 0.6 | 0.6 | 0.4 |
(2)用线性回归分析的方法,预测小李该月6号打6小时篮球的投篮命中率.$\left\{\begin{array}{l}\hat b=\frac{{\sum_{i=1}^n{({x_i}-\overline x)({y_i}-\overline y)}}}{{\sum_{i=1}^n{{{({x_i}-\overline x)}^2}}}}=\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x\overline y}}}{{\sum_{i=1}^n{x_i^2-n{{\overline x}^2}}}}\\ \hat a=\overline y-\hat b\overline x\end{array}\right.$.
18.下列结论错误的是( )
0 224093 224101 224107 224111 224117 224119 224123 224129 224131 224137 224143 224147 224149 224153 224159 224161 224167 224171 224173 224177 224179 224183 224185 224187 224188 224189 224191 224192 224193 224195 224197 224201 224203 224207 224209 224213 224219 224221 224227 224231 224233 224237 224243 224249 224251 224257 224261 224263 224269 224273 224279 224287 266669
| A. | 命题“若p,则q”与命题“若¬q,则¬p”互为逆否命题 | |
| B. | 命题p:?x∈[0,1],ex≥1;命q:?x∈R,x2+x+1<0,则p∨q为真 | |
| C. | 命题“?x∈R,2x>0”的否定是“?x0∈R,2x≤0” | |
| D. | “若am2<bm2,则a<b”的逆命题为真命题 |
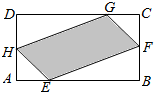 如图,有一块矩形空地,要在这块空地上开辟一个内接四边形为绿地,使其四个顶点分别落在矩形的四条边上,已知AB=4,BC=2,且AE=AH=CF=CG,设AE=x,绿地面积为y.
如图,有一块矩形空地,要在这块空地上开辟一个内接四边形为绿地,使其四个顶点分别落在矩形的四条边上,已知AB=4,BC=2,且AE=AH=CF=CG,设AE=x,绿地面积为y.