题目内容
20．已知函数f（x）是定义在R上的奇函数，若x＜0时，f（x）=x2-2x，求函数f（x）的解析式．分析 根据函数奇偶性的性质，利用对称性进行求解即可．
解答 解：∵函数f（x）是定义在R上的奇函数，
∴f（0）=0，
若x＞0，则-x＜0，即f（-x）=x2+2x，
∵f（x）是定义在R上的奇函数，
∴f（-x）=x2+2x=-f（x），
即f（x）=-x2-2x，x＞0，
则函数的解析式为f（x）=$\left\{\begin{array}{l}{x^2}-2x\\ 0\\-{x^2}-2x\end{array}\right.$，$\begin{array}{l}x＜0\\ x=0\\ x＞0\end{array}$．
点评 本题主要考查函数解析式的求解，利用函数奇偶性的性质是解决本题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
11．由幂函数y=$\sqrt{x}$和幂函数y=x3图象围成的封闭图形的面积为（ ）
| A． | $\frac{1}{12}$ | B． | $\frac{1}{4}$ | C． | $\frac{1}{3}$ | D． | $\frac{5}{12}$ |
8．已知复数z=$\frac{3-i}{2+i}$（i为虚数单位），则|z|=（ ）
| A． | $\sqrt{2}$ | B． | 2 | C． | $\sqrt{3}$ | D． | $\frac{3}{2}$ |
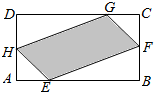如图，有一块矩形空地，要在这块空地上开辟一个内接四边形为绿地，使其四个顶点分别落在矩形的四条边上，已知AB=4，BC=2，且AE=AH=CF=CG，设AE=x，绿地面积为y．