设函数f(x)=lg(x2+ax﹣a﹣1),给出下述命题:
①函数f(x)的值域为R;②函数f(x)有最小值;
③当a=0时,函数f(x)为偶函数;④若f(x)在区间[2,+∞)上单调递增,则实数a的取值范围a≥﹣4.
正确的命题是( )
|
| A. | ①③ | B. | ②③ | C. | ②④ | D. | ③④ |
设f(x)是定义在R上的偶函数,且f(2+x)=f(2﹣x),当x∈[﹣2,0)时,f(x)=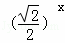 ﹣1,若在区间(﹣2,6)内的关于x的方程f(x)﹣loga(x+2)=0(a>0且a≠1)恰有4个不同的实数根,则实数a的取值范围是( )
﹣1,若在区间(﹣2,6)内的关于x的方程f(x)﹣loga(x+2)=0(a>0且a≠1)恰有4个不同的实数根,则实数a的取值范围是( )
|
| A. | ( | B. | (1,4) | C. | (1,8) | D. | (8,+∞) |
 ,1)
,1) ,x∈(0,4),当x=a时,f(x)取得最小值b,则在直角坐标系中函数g(x)=
,x∈(0,4),当x=a时,f(x)取得最小值b,则在直角坐标系中函数g(x)= 的图象为( )
的图象为( )




 的反函数
的反函数 ________________.
________________. 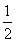 ,用水越多洗掉的农药量也越多,但总还有农药残留在蔬菜上.设用
,用水越多洗掉的农药量也越多,但总还有农药残留在蔬菜上.设用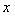 单位量的水清洗一次以后,蔬菜上残留的农药量与本次清洗前残留的农药量之比为函数
单位量的水清洗一次以后,蔬菜上残留的农药量与本次清洗前残留的农药量之比为函数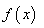 .⑴试规定
.⑴试规定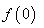 的值,并解释其实际意义;
的值,并解释其实际意义;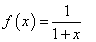 ,现有
,现有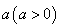 单位量的水,可以清洗一次,也可以把水平均分成两份后清洗两次.试问用那种方案清洗后蔬菜上残留的农药量比较少?说明理由.
单位量的水,可以清洗一次,也可以把水平均分成两份后清洗两次.试问用那种方案清洗后蔬菜上残留的农药量比较少?说明理由. (x∈[﹣π,π])的最大值为M,最小值为m,则M+m= .
(x∈[﹣π,π])的最大值为M,最小值为m,则M+m= . 是奇函数,定义域为区间D(使表达式有意义的实数x 的集合).
是奇函数,定义域为区间D(使表达式有意义的实数x 的集合). (a、b是常数且a>0,a≠1)在区间[-
(a、b是常数且a>0,a≠1)在区间[- ,0]上有ymax=3,ymin=
,0]上有ymax=3,ymin= ,试求a和b的值.
,试求a和b的值.