题目内容
已知函数 是奇函数,定义域为区间D(使表达式有意义的实数x 的集合).
是奇函数,定义域为区间D(使表达式有意义的实数x 的集合).
(1)求实数m的值,并写出区间D;(2)若底数a>1,试判断函数y=f(x)在定义域D内的单调性,并说明理由;
(3)当x∈A=[a,b)(A⊆D,a是底数)时,函数值组成的集合为[1,+∞),求实数a、b的值.
解(1)∵y=f(x)是奇函数,∴对任意x∈D,有f(x)+f(﹣x)=0,即 .(2分)化简此式,得(m2﹣1)x2﹣(2m﹣1)2+1=0.又此方程有无穷多解(D是区间),必有
.(2分)化简此式,得(m2﹣1)x2﹣(2m﹣1)2+1=0.又此方程有无穷多解(D是区间),必有 ,解得m=1.(4分)∴
,解得m=1.(4分)∴ .(5分)
.(5分)
(2)当a>1时,函数 上是单调减函数.理由:令
上是单调减函数.理由:令 .
.
易知1+x在D=(﹣1,1)上是随x增大而增大, 在D=(﹣1,1)上是随x增大而减小,(6分)
在D=(﹣1,1)上是随x增大而减小,(6分)
故 在D=(﹣1,1)上是随x增大而减小.(8分)
在D=(﹣1,1)上是随x增大而减小.(8分)
于是,当a>1时,函数 上是单调减函数.(10分)
上是单调减函数.(10分)
(3)∵A=[a,b)⊆D,∴0<a<1,a<b≤1.(11分)
∴依据(2)的道理,当0<a<1时,函数 上是增函数,(12分)
上是增函数,(12分)
即 ,解得
,解得 .(14分)
.(14分)
若b<1,则f(x)在A上的函数值组成的集合为 ,不满足函数值组成的集合是[1,+∞)的要求.(也可利用函数的变化趋势分析,得出b=1)∴必有b=1.(16分)因此,所求实数a、b的值是
,不满足函数值组成的集合是[1,+∞)的要求.(也可利用函数的变化趋势分析,得出b=1)∴必有b=1.(16分)因此,所求实数a、b的值是 .
.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
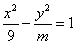 的一个焦点在圆
的一个焦点在圆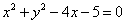 上,则双曲线的渐近线方程为
上,则双曲线的渐近线方程为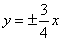 B.
B.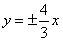 C.
C.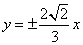 D.
D.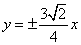
 ,若
,若 ,则实数
,则实数 的取值范围是 .
的取值范围是 . ,
, 是由
是由 轴和曲线
轴和曲线 及该曲线在点
及该曲线在点 处的切线所围成的封闭区域,则
处的切线所围成的封闭区域,则 在
在
 ( )
( ) 中,常数
中,常数 那么
那么 的解集为
的解集为 B.
B. C.
C. D.
D.
 .
. ,解方程
,解方程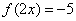 ;
;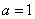 ,判断
,判断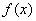 的单调区间并证明;
的单调区间并证明; ,使
,使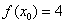 ,求实数
,求实数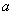 的取值范围 .
的取值范围 .