某中学研究性学习小组,为了考查高中学生的作文水平与爱看课外书的关系,在本校高三年级随机调查了50名学生.调查结果表明:在爱看课外书的25人中有18人作文水平好,另7人作文水平一般;在不爱看课外书的25人中有6人作文水平好,另19人作文水平一般.
(1)试根据以上数据完成以下2×2列联表,并运用独立性检验思想,指出有多大把握认为中学生的作文水平与爱看课外书有关系?
高中学生的作文水平与爱看课外书的2×2列联表
|
| 爱看课外书 | 不爱看课外书 | 总计 |
| 作文水平好 | |||
| 作文水平一般 | |||
| 总计 |
(2)将其中某5名爱看课外书且作文水平好的学生分别编号为1、2、3、4、5,某5名爱看课外书且作文水平一般的学生也分别编号为1、2、3、4、5,从这两组学生中各任选1人进行学习交流,求被选取的两名学生的编号之和为3的倍数或4的倍数的概率.
附表:
| P(K2≥k)或P(χ2≥k) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
K2(或χ2)=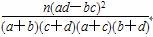
在某医学实验中,某实验小组为了分析某药物用药量与血液中某种抗体水平的关系,选取六只实验动物进行血检,得到如下资料:
| 动物编号 | 1 | 2 | 3 | 4 | 5 | 6 |
| 用药量x(单位) | 1 | 3 | 4 | 5 | 6 | 8 |
| 抗体指标y(单位) | 3.4 | 3.7 | 3.8 | 4.0 | 4.2 | 4.3 |
记s为抗体指标标准差,若抗体指标落在(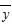 -s,
-s,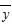 +s)内,则称该动物为有效动物,否则称为无效动物.研究方案规定先从六只动物中选取两只,用剩下的四只动物的数据求线性回归方程,再对被选取的两只动物数据进行检验.
+s)内,则称该动物为有效动物,否则称为无效动物.研究方案规定先从六只动物中选取两只,用剩下的四只动物的数据求线性回归方程,再对被选取的两只动物数据进行检验.
(1)求选取的两只动物都是有效动物的概率;
(2)若选取的是编号为1和6的两只动物,且利用剩余四只动物的数据求出y关于x的线性回归方程为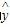 =0.17x+a,试求出a的值;
=0.17x+a,试求出a的值;
(3)若根据回归方程估计出的1号和6号动物抗体指标数据与检验结果误差都不超过抗体指标标准差,则认为得到的线性回归方程是可靠的.试判断(2)中所得线性回归方程是否可靠.
参考公式:样本数据x1,x2,…,xn的标准差:
S=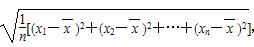 ,其中
,其中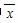 为样本平均数.
为样本平均数.
某车间为了规定工时定额,需要确定加工零件所花费的时间,为此作了四次试验,得到的数据如下:
| 零件的个数x(个) | 2 | 3 | 4 | 5 |
| 加工的时间y(小时) | 2.5 | 3 | 4 | 4.5 |

(1)在给定的坐标系中画出表中数据的散点图;
(2)求出y关于x的线性回归方程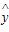 =bx+a,并在坐标系中画出回归直线;
=bx+a,并在坐标系中画出回归直线;
(3)试预测加工10个零件需要多少时间?
(注:b= ,a=
,a= -b
-b )
)
某车间为了规定工时定额,需要确定加工零件所花费的时间,为此进行了5次试验.根据收集到的数据(如下表),由最小二乘法求得回归直线方程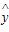 =0.67x+54.9.
=0.67x+54.9.
| 零件数x(个) | 10 | 20 | 30 | 40 | 50 |
| 加工时间y(min) | 62 |
| 75 | 81 | 89 |
表中一个数据模糊不清,经推断,该数据的值为______.
对四组数据进行统计,获得以下散点图,关于其相关系数的比较,正确的是( )

A.r2<r4<0<r3<r1 B.r4<r2<0<r1<r3
C.r4<r2<0<r3<r1 D.r2<r4<0<r1<r3
已知x与y之间的几组数据如下表:
| x | 1 | 2 | 3 | 4 | 5 | 6 |
| y | 0 | 2 | 1 | 3 | 3 | 4 |
假设根据上表数据所得线性回归直线方程为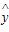 =
=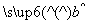 x+
x+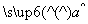 .若某同学根据上表中的前两组数据(1,0)和(2,2)求得的直线方程为y=b′x+a′,则以下结论正确的是( )
.若某同学根据上表中的前两组数据(1,0)和(2,2)求得的直线方程为y=b′x+a′,则以下结论正确的是( )
A.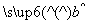 >b′,
>b′,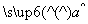 >a′ B.
>a′ B.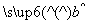 >b′,
>b′,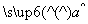 <a′
<a′
C.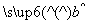 <b′,
<b′,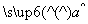 >a′ D.
>a′ D.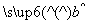 <b′,
<b′,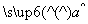 <a′
<a′
为了分析某个高三学生的学习状态,对其下一阶段的学习提供指导性建议.现对他前7次考试的数学成绩x、物理成绩y进行分析.下面是该生7次考试的成绩:
| 数学 | 88 | 83 | 117 | 92 | 108 | 100 | 112 |
| 物理 | 94 | 91 | 108 | 96 | 104 | 101 | 106 |
(1)他的数学成绩与物理成绩哪个更稳定?请给出你的证明;
(2)已知该生的物理成绩y与数学成绩x是线性相关的,若该生的物理成绩达到115分,请你估计他的数学成绩大约是多少?并请你根据物理成绩与数学成绩的相关性,给出该生在学习数学、物理上的合理性建议.
在2012年8月15日那天,某市物价部门对本市的5家商场的某商品的一天销售量及其价格进行调查,5家商场的售价x元和销售量y件之间的一组数据如下表所示:
| 价格x | 9 | 9.5 | m | 10.5 | 11 |
| 销售量y | 11 | n | 8 | 6 | 5 |
由散点图可知,销售量y与价格x之间有较强的线性相关关系,其线性回归直线方程是: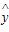 =-3.2x+40,且m+n=20,则其中的n=________.
=-3.2x+40,且m+n=20,则其中的n=________.
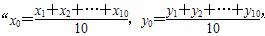 的( )
的( )