已知f1（x）=sinx+cosx，f2（x）=f1′（x），f3（x）=f2′（x）…fn（x）=fn-1′（x）（n∈N+，n≥2），记f1（
）+f2（
）+…+f2013（
）等于（ ）
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
| A、1 | B、-1 | C、0 | D、-2 |
| 1 |
| 3 |
| ∫ |
-
|
A、
| ||||
B、
| ||||
C、
| ||||
D、-
|
曲线y=e-x（e为自然对数的底数）在点M（1，e-1）处的切线l与x轴、y轴所围成的三角形的面积为（ ）
A、
| ||
B、
| ||
| C、e | ||
| D、2e |
若图程序输出的y=3，则输入的x为（ ）
| A、2 | B、-2 | C、2或-2 | D、8 |
圆x2+y2-6x=0与圆x2+y2+8y+12=0的位置关系是（ ）
| A、相离 | B、相交 | C、外切 | D、内切 |
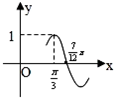已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜| π |
| 2 |
A、先把各点的横坐标缩短到原来的
| ||||
B、先把各点的横坐标伸长到原来的2倍，再向右平移
| ||||
C、先向右平移
| ||||
D、先向右平移
|
函数y=
-
，x∈[1，4]的最小值为（ ）
| x |
| 1 |
| x |
A、
| ||
B、-
| ||
C、
| ||
| D、0 |
已知函数f（x）是[-1，1]上的减函数，α、β是锐角三角形的两个内角，且α≠β，则下列不等式中正确的是（ ）
| A、f（sinα）＞f（cosβ） |
| B、f（cosα）＜f（cosβ） |
| C、f（cosα）＞f（sinβ） |
| D、f（sinα）＜f（sinβ） |
以下是解决数学问题的思维过程的流程图：
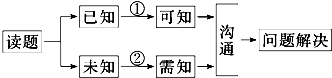
在此流程图中，①②两条流程线与“推理与证明”中的思维方法匹配正确的是（ ）
在此流程图中，①②两条流程线与“推理与证明”中的思维方法匹配正确的是（ ）
| A、①-综合法，②-分析法 |
| B、①-分析法，②-综合法 |
| C、①-综合法，②-反证法 |
| D、①-分析法，②-反证法 |