已知E为不等式组
,表示区域内的一点,过点E的直线l与圆M:(x-1)2+y2=9相交于A,C两点,过点E与l垂直的直线交圆M于B、D两点,当AC取最小值时,四边形ABCD的面积为( )
|
A、4
| ||
B、6
| ||
C、12
| ||
| D、12 |
设函数f(x)=3sin(2x+
)+1,将y=f(x)的图象向右平移φ(φ>0)个单位,使得到的图象关于y轴对称,则φ的最小值为( )
| π |
| 4 |
A、
| ||
B、
| ||
C、
| ||
D、
|
多面体MN-ABCD的底面ABCD为矩形,其正视图和侧视图如图,其中正视图为等腰梯形,侧视图为等腰三角形,则该多面体的体积是( )
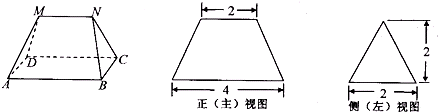

A、
| ||||
B、
| ||||
C、
| ||||
D、
|
平面向量
=(2,1),
=(m2,m),若“m=2”是“
与
共线”的( )
| a |
| b |
| a |
| b |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
已知l,m,n是空间三条不同直线,命题p:若l⊥m,l⊥n,则m∥n;命题q:若三条直线l,m,n两两相交,则直线l,m,n共面,则下列命题为真命题的是( )
| A、p∧q | B、p∨q |
| C、p∨(¬q) | D、(¬p)∧q |
设a,b是关于x的方程x2sinθ+xcosθ-2=0(θ∈R)的两个互异实根,直线l过点A(a,a2),B(b,b2),则坐标原点O到直线l的距离是( )
| A、2 |
| B、2|tanθ| |
| C、2|cotθ| |
| D、2|sinθcosθ| |
已知关于x的方程lnx=mx,x∈(0,a),若存在a,m,使此方程有两个不同的实数解,则称实数对(a,m)为此方程的“D-S-P”,则在(
,-
),(
,
),(2e,
),(e2,
)中,“D-S-P”点有( )
| 1 |
| 2 |
| 1 |
| e |
| e |
| 1 | ||
3
|
| 2ln2 |
| e |
| 5 |
| 2e2 |
| A、1个 | B、2个 | C、3个 | D、4个 |
设变量x,y满足约束条件
,则z=2x-y的最大值为( )
|
| A、-3 | ||
B、
| ||
| C、5 | ||
| D、6 |
已知函数f(x)=2x-1-log
x,则f(x)的零点的个数为( )
| 1 |
| 2 |
| A、0 | B、1 | C、2 | D、3 |
若不等式组
表示的平面区域内存在点M(x0,y0),满足2x0+y0=6,则实数m的取值范围是( )
|
| A、[1,+∞) |
| B、[0,1] |
| C、(0,1) |
| D、[0,2] |