如图，四棱锥A-BCDE中，底面BCDE为矩形，侧面ABC⊥底面BCDE，BC=2，CD=| 2 |
（1）证明：AD⊥CE；
（2）求二面角A-CE-B的正切值．
已知椭圆C：1+C271+C272+C2727除以3所得余数为（ ）
| A、0 | B、1 | C、2 | D、3 |
α、β是两个不同的平面，m、n是平面α及β之外的两条不同直线，给出四个论断：①m⊥n；②α⊥β；③n⊥β；④m⊥α．以其中三个论断作为条件，余下一个作为结论，其中正确命题的个数是（ ）
| A、1个 | B、2个 | C、3个 | D、4个 |
如图所示是《函数的应用》的知识结构图，如果要加入“用二分法求方程的近似解”，则应该放在（ ）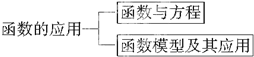
| A、“函数与方程”的上位 |
| B、“函数与方程”的下位 |
| C、“函数模型及其应用”的上位 |
| D、“函数模型及其应用”的下位 |
已知x，y∈R，若lne-1i+2=y+xi，则x3+y=（ ）
| A、9 | B、3 | C、1 | D、2 |
没有信息损失的统计图表是（ ）
| A、条形统计图 | B、扇形统计图 |
| C、折线统计图 | D、茎叶图 |
已知直线l⊥平面α，直线m⊆平面β，给出下列命题，其中正确的是（ ）
①α∥β⇒l⊥m
②α⊥β⇒l∥m
③l∥m⇒α⊥β
④l⊥m⇒α∥β
①α∥β⇒l⊥m
②α⊥β⇒l∥m
③l∥m⇒α⊥β
④l⊥m⇒α∥β
| A、②④ | B、②③④ |
| C、①③ | D、①②③ |