已知△ABC是边长为2的等边三角形，在平面ABC所在平面上有一点P，M是AP的中点，满足（
AC
-
AM
）•（
AB
-
AP
）=0，则|
BM
|的最小值为（　　）
A、
7
-
3
2
B、
3
-1
2
C、
3
2
D、
7
2
有以下命题：
①如果向量
a
，
b
与任何向量不能构成空间的一个基底，那么
a
，
b
的关系是不共线；
②O，A，B，C为空间四点，且向量
OA
，
OB
，
OC
不构成空间的一个基底，那么点O，A，B，C一定共面；
③若向量
p
空间的一个单位正交基底
a
，
b
，
c
下的坐标为（1，2，3），那么向量
p
在基底
a
+
b
，
a
-
b
，
c
下的坐标为（
3
2
，-
1
2
，3）．
④若A，B，C三点不共线，O是平面ABC外一点，
OM
=
1
3
OA
+
1
3
OB
+
1
3
OC
，则点M一定在平面ABC上，且在△ABC的内部．
其中正确的命题是（　　）
A、①②B、①③④
C、②③④D、①②③
已知O为锐角△ABC的外心，AB=6，AC=4，若
AO
=x
AB
+y
AC
，且x+4y=2，则cos∠BAC=（　　）
A、
1
6
B、-
1
3
C、-
1
4
D、
1
3
命题“x∈Z，都有x2-2x+a＞0”的否定是（　　）
A、?x∈Z，使x2-2x+a≤0
B、?x∈Z，使x2-2x+a＞0
C、?x∈Z，都有x2-2x+a＞0
D、不存在?x∈Z，使x2-2x+a＞0
已知球的表面积为144π，则球的体积为（　　）
A、48πB、192π
C、162πD、288π
将函数y=2sin
π
3
x的图象上每一点向右平移1个单位，再将所得图象上每一点的横坐标扩大为原来的
π
3
倍（纵坐标保持不变），得到函数y=f（x）的图象，则f（x）的一个解析式是（　　）
A、y=2sin（x+
π
3
）
B、y=2sin（x-
π
3
）
C、y=2sin（x+1）
D、y=2sin（x-1）
一所中学有高一、高二、高三共三个年级的学生900名，其中高一学生400名，高二学生300名，高三学生200名．如果通过分层抽样的方法从全体高中学生中抽取一个容量为45人的样本，那么应当从三年级的学生中抽取的人数是（　　）
A、30 10 5
B、25 15 15
C、20 15 10
D、15 15 15
在△ABC中，内角A、B、C的对边分别是a、b、c，若cosB=
1
4
，
sinC
sinA
=2，且S△ABC=
15
4
，则b=（　　）
A、4B、3C、2D、1
己知一个正方体的所有顶点在一个球面上，若球的体积为
9π
2
，则正方体的棱长为（　　）
A、
6
2
B、
3
2
C、
3
D、1
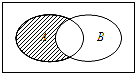已知全集U=R，集合A={0，1，2}，B={2，3，4}，如图阴影部分所表示的集合为（　　）
A、{2}
B、{0，1}
C、{3，4}
D、{0，1，2，3，4}
 0  208595  208603  208609  208613  208619  208621  208625  208631  208633  208639  208645  208649  208651  208655  208661  208663  208669  208673  208675  208679  208681  208685  208687  208689  208690  208691  208693  208694  208695  208697  208699  208703  208705  208709  208711  208715  208721  208723  208729  208733  208735  208739  208745  208751  208753  208759  208763  208765  208771  208775  208781  208789  266669 

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网