题目内容
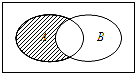已知全集U=R，集合A={0，1，2}，B={2，3，4}，如图阴影部分所表示的集合为（ ）| A、{2} |
| B、{0，1} |
| C、{3，4} |
| D、{0，1，2，3，4} |
考点：Venn图表达集合的关系及运算
专题：集合
分析：阴影部分表示的集合为A∩（∁UB），然后根据集合的基本运算，即可得到结论．
解答：
解：阴影部分表示的集合为A∩（∁UB），
∵A={0，1，2}，B={2，3，4}，
∴A∩（∁UB）={0，1}，
故选：B
∵A={0，1，2}，B={2，3，4}，
∴A∩（∁UB）={0，1}，
故选：B
点评：本题主要考查集合的基本运算，根据Venn图确定集合关系是解决本题的关键，比较基础．
练习册系列答案
相关题目
已知命题p：?α∈（0，
），sinα+cosα=
；命题q：?x∈[0，+∞），x+cosx≥1，则下列命题中是真命题的为（ ）
| π |
| 2 |
| 1 |
| 2 |
| A、p∧q | B、￢p∧q |
| C、p∨￢q | D、￢p∧￢q |
二项式（2x-
）6的展开式中的常数项是（ ）
| 1 |
| x |
| A、20 | B、-20 |
| C、160 | D、-160 |
已知集合A={x|-1＜x≤2}，B={x|y=
-1+ln（2-x）}，则A∩B=（ ）
| x-1 |
| A、（1，2] |
| B、[1，2] |
| C、（1，2） |
| D、[1，2） |
设x、y 满足线性约束条件
，则目标函数z=x-y的最大值为（ ）
|
| A、-2 | B、-1 | C、0 | D、2 |
已知球的表面积为144π，则球的体积为（ ）
| A、48π | B、192π |
| C、162π | D、288π |
定积分
cos2xdx等于（ ）
| ∫ |
-
|
A、
| ||
B、
| ||
C、
| ||
D、
|
如果命题“￢（p∨q）”为假命题，则（ ）
| A、p、q均为假命题 |
| B、p、q均为真命题 |
| C、p、q中至少有一个为假命题 |
| D、p、q中至少有一个为真命题 |
