若函数f（x），g（x）的定义域和值域都是R，则f（x）＞g（x）（x∈R）成立的充要条件是（ ）
| A、?x0∈R，f（x0）＞g（x0） |
| B、有无穷多个x∈R，使得f（x）＞g（x） |
| C、?x∈R，f（x）＞g（x）+1 |
| D、R中不存在x使得f（x）≤g（x） |
定义在R上的偶函数f（x）的部分图象如图所示，则区间（-2，0）上下列函数的图象与f（x）的单调性相同的个数是（ ）（Ⅰ）y=x2+1
（Ⅱ）y=|x|+1
（Ⅲ）y=
|
（Ⅳ）y=sinx．
| A、0 | B、1 | C、2 | D、3 |
要得到函数y=2sin（2x-
）的图象，只需要将函数y=2sin2x的图象向（ ）平移（ ）个单位．括号中应填入（ ）
| π |
| 2 |
A、左
| ||
B、右
| ||
C、左
| ||
D、右
|
要得到函数f（x）=-
f（
-x）-sinx的图象，只需将g（x）=sinx的图象（ ）
| 3 |
| π |
| 2 |
A、向左平移
| ||
B、向右平移
| ||
C、向左平移
| ||
D、向右平移
|
若双曲线
-y2=1上的点到右准线的距离是到右焦点距离的
，则m=（ ）
| x2 |
| m |
| 1 |
| 2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知函数y=sin（ωx+φ）（ω＞0，-
＜φ＜
）的部分图象如图所示，则（ ）
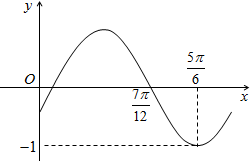
| π |
| 2 |
| π |
| 2 |
A、ω=2，φ=-
| ||
B、ω=2，φ=
| ||
C、ω=1，φ=-
| ||
D、ω=1，φ=
|
将函数y=sinx（其中x∈R）图象F上各点的横坐标缩短到原来的
倍（纵坐标不变），得到图象F1，再将F1向右平移
个单位得到图象F2，则F2的函数表达式为（ ）
| 1 |
| 2 |
| π |
| 6 |
A、y=sin（
| ||||
B、y=sin（2x-
| ||||
C、y=sin（2x-
| ||||
D、y=sin（2x+
|
命题甲：p或非q是假命题，命题乙：p或q是真命题．则命题甲是命题乙的（ ）
| A、充分非必要条件 |
| B、必要非充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
i是虚数单位，
的虚部等于（ ）
| i |
| 1+i |
| A、0 | ||
B、-
| ||
| C、1 | ||
D、
|