已知A(-2,0),B(0,2),实数k是常数,M,N是圆x2+y2+kx=0上两个不同点,P是圆x2+y2+kx=0上的动点,如果M,N关于直线x-y-1=0对称,则△PAB面积的最大值是( )
A、3-
| ||
| B、4 | ||
| C、6 | ||
D、3+
|
已知函数f(x)=sinωx+cosωx(ω>0),如果存在实数x1,使得对任意的实数x,都有f(x1)≤f(x)≤f(x1+2013)成立,则ω的最小值为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
以下命题(m,l表示直线,α表示平面)正确的个数有( )
①若l∥m,m?α,则l∥α;②若l∥α,m?α,则l∥m
③若l⊥α,m?α,则l⊥m;④若l⊥α,m⊥l,则m∥α.
①若l∥m,m?α,则l∥α;②若l∥α,m?α,则l∥m
③若l⊥α,m?α,则l⊥m;④若l⊥α,m⊥l,则m∥α.
| A、0个 | B、1个 | C、2个 | D、3个 |
设p:f(x)=x3+2x2+mx+1在(-∞,+∞)内单调递增,q:m≥2,则p是q的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分又不必要条件 |
在△ABC中,角A,B,C对应边分别是a,b,c,a=5,b=8,C=60°,则
•
等于( )
| BC |
| CA |
| A、40 | B、-40 |
| C、20 | D、-20 |
设函数f(x)=
,则
(a≠b)的值为( )
|
| (a+b)+(a-b)•f(a-b) |
| 2 |
| A、a | B、b |
| C、a,b中较小的数 | D、a,b中较大的数 |
若实数x,y满足不等式组
,则目标函数z=2x+y( )
|
| A、有最小值3,无最大值 |
| B、有最大值12,无最小值 |
| C、有最大值12,最小值3 |
| D、既无最大值,也无最小值 |
已知
=
,则a•b=( )
| lim |
| x→1 |
| x-1 |
| x2+ax+b |
| 1 |
| 4 |
| A、-6 | B、-5 | C、5 | D、6 |
已知某个几何体的三视图,根据图中标出的尺寸,这个几何体的体积是( )


A、(
| ||||
B、(
| ||||
C、(
| ||||
D、(
|
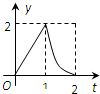
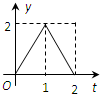
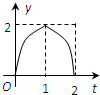
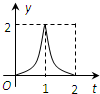
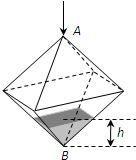 如图所示,连结棱长为2cm的正方体各面的中心得一个多面体容器,从顶点A处向该容器内注水,注满为止.已知顶点B到水面的高度h以每秒1cm匀速上升,记该容器内水的体积V(cm3)与时间T(S)的函数关系是V(t),则函数V(t)的导函数y=V′(t)的图象大致是( )
如图所示,连结棱长为2cm的正方体各面的中心得一个多面体容器,从顶点A处向该容器内注水,注满为止.已知顶点B到水面的高度h以每秒1cm匀速上升,记该容器内水的体积V(cm3)与时间T(S)的函数关系是V(t),则函数V(t)的导函数y=V′(t)的图象大致是( )